Cho ΔABC vuông ở A . Gọi M là trung điểm của cạnh AC ; trên tia đối của tia MB lấy điểm E sao cho ME = MB
a) CM : ΔAMB = ΔCME
b) So sánh CE và BC
c) So sánh \(\widehat{ABM}\) và \(\widehat{MBC}\)
d) CM : AE // BC
B1. Cho ΔABC có Aˆ=90∘. AB = AC, điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho AD = AE. Đường thẳng qua D và vuông góc với BE cắt đường thẳng CA ở K. CMR: AK = AC
B2. Cho ΔABC, I là trung điểm của AB, đường thẳng qua I và song song với BC cắt AC ở K. Đường thẳng qua K và song song với AB cắt BC ở H. CMR
a) KH = IB
b) AK = KC
B3. Cho ΔABC có Aˆ = 60∘. Tia phân giác của Bˆ cắt AC ở D, tia phân giác của Cˆ cắt AB ở E. Gọi O là giao điểm của BD và CE.
a) Tính BOCˆ
b) C/m CD = OE
B4. Cho ΔABC. Ở phía ngoài ΔABC vẽ các tam giác vuông tại A là ABD và ACE có AB = AD, AC = AE. Kẻ AH vuông góc với BC, gọi I là giao điểm của HA và DE. CMR: DI = IE
Giúp em với !! T7 phải nộp rồiii
Cho ΔABC cân ở A. Trên cạnh BC lấy điểm M, N sao cho BM = CN < BC/2. Kẻ ME vuông góc với AB, NF vuông góc với AC (E ϵ AB, F ϵ AC), EM cắt FN tại H. Chứng minh:
a) ΔABM = ΔACN.
b) Gọi D là trung điểm của MN. Chứng minh AD là tia phân giác của góc BAC.
c) EF // BC.
d) Chứng mình: A, D, H thẳng hàng.
Bài 1: Cho 2 tam giác vuông, ΔABC vuông tại A, MNP vuông tại M. Biết ΔABC = ΔMNP, AB= 20cm, AC= 15cm. Tính các cạnh của ΔMNP
Bài 2: Cho ΔABC có AB=AC. Gọi H là trung điểm của cạnh BC a) Chứng minh ΔABH = ΔACH b) Chứng minh AH vuông ∠ BC c) Trên tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD = CE. Chứng minh ΔHAD = ΔHAE d) Gọi K là trung điểm của DE. Chứng minh 3 điểm A, H, K thẳng hàng
ANH CHỊ GIÚP EM VỚI CHIỀU EM NỘP RỒI
Cho ΔABC vuông tại A (AB < AC), đường cao AH. Trên cạnh AC lấy điểm D sao cho AD = AB. Gọi O là trung điểm của BD. . Vẽ (O) đường kính BD cắt cạnh BC tại điểm thứ hai K.
a, C/m: CK.CB = CD.CA
b, Tính ˆAHO
a, Xét đường tròn (O) có: \(\Delta\)BKD nội tiếp; BD là đường kính
\(\Rightarrow\) \(\Delta\)BKD vuông tại K (sự xác định đường tròn)
\(\Rightarrow\) BK \(\perp\) KD
Mà C \(\in\) BK \(\Rightarrow\) CK \(\perp\) KD
Xét \(\Delta\)CKD và \(\Delta\)CAB có:
\(\widehat{CKD}=\widehat{CAB}=90^o\)
\(\widehat{C}\) chung
\(\Rightarrow\) \(\Delta\)CKD ~ \(\Delta\)CAB (gg)
\(\Rightarrow\) \(\dfrac{CK}{CA}=\dfrac{CD}{CB}\) (tỉ số đồng dạng)
\(\Rightarrow\) CK.CB = CD.CA (đpcm)
b, Xét tam giác ABD có: AB = AD (gt)
\(\Rightarrow\) \(\Delta\)ABD cân tại A (dhnb)
Mà AO là trung tuyến ứng với BD của \(\Delta\)ABD (O là tâm của đường tròn đk BD)
\(\Rightarrow\) AO là đường cao ứng với BD (tính chất tam giác cân)
\(\Rightarrow\) \(\widehat{AOB}\) = 90o
Xét tứ giác BHOA có: \(\widehat{BHA}=\widehat{BOA}=90^o\) (AH là đường cao; cmt)
Hai góc có đỉnh kề nhau cùng nhìn cạnh AB dưới 1 góc vuông ko đổi
\(\Rightarrow\) BHOA là tứ giác nội tiếp (dhnb tứ giác nội tiếp)
\(\Rightarrow\) \(\widehat{AHO}=\widehat{ABO}\) (2 góc nội tiếp cùng chắn \(\stackrel\frown{AO}\)) (1)
Xét tam giác ABD cân tại A có: \(\widehat{BAD}=90^o\) (tam giác ABD vuông tại A)
\(\Rightarrow\) Tam giác ABD vuông cân tại A
\(\Rightarrow\) \(\widehat{ABD}\) = 45o (t/c tam giác vuông cân) (2)
Từ (1) và (2) \(\Rightarrow\) \(\widehat{AHO}=45^o\)
Chúc bn học tốt!
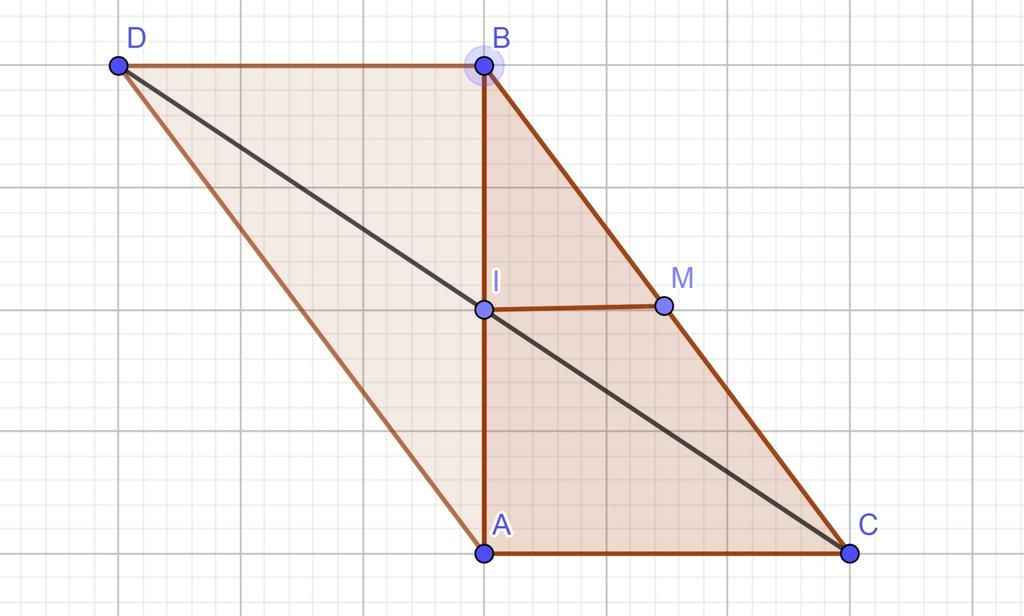
Cho tam giác ABC có A= 90 độ, AC = 5cm, BC = 13cm. Gọi I là trung điểm của cạnh AB, D là điểm đối xứng với C qua I.
a) Tứ giác ADBC là hình gì? Vì sao?
b) Gọi M là trung điểm của cạnh BC. Chứng minh: MI vuông góc với AB. Tính diện tích ΔABC.
a) Xét tứ giác \(ADBC\) ta có :
\(IB=IA\left(g.t\right)\)
\(IC=IC\) ( \(D\) đối xứng qua \(I\))
Vì tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường
Vậy tứ giác \(ADBC\) là hình bình hành
b) Xét \(\Delta ABC\) ta có :
\(IA=IB\left(g.t\right)\)
\(MB=MC\left(g.t\right)\)
\(\Rightarrow IM\) là đường trung bình \(\Delta ABC\)
Do đó : \(IM\text{/ / }AC\)
Mà \(AB\text{⊥}AC\left(A=90^o\right)\)
Vậy \(IM\text{⊥}AB\)
Áp dụng định lí pytago \(\Delta ABC\) ta có :
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{13^2-5^2}=12\left(cm\right)\)
\(S_{\Delta ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.13.5=30\left(cm^2\right)\)
Cho ΔABC vuông tại A từ trung điểm M của cạnh BC, kẻ MD và ME lần lượt vuông góc với AB và AC ( E ∈ AB, D ∈ AC). Lấy điểm F đối xứng với M qua Ea) Chứng minh tứ giác AMCF là hình thoib) Tìm điều kiện để ΔABC để tứ giác AMCE là hình vuôngc) Gọi I là trung điểm của EM. Chứng minh I là trung điểm của CD
a) Xét ΔAMF có
AE là đường cao ứng với cạnh MF(\(AE\perp MF\))
AE là đường trung tuyến ứng với cạnh MF(E là trung điểm của MF)
Do đó: ΔAMF cân tại A(Định lí tam giác cân)
hay AM=AF(1)
Xét ΔCFM có
CE là đường cao ứng với cạnh MF(\(CE\perp MF\))
CE là đường trung tuyến ứng với cạnh MF(E là trung điểm của MF)
Do đó: ΔCFM cân tại C(Định lí tam giác cân)
hay CM=CF(2)
Vì ΔABC vuông tại A(gt) có AM là đường trung tuyến ứng với cạnh huyền BC(M là trung điểm của BC)
nên \(AM=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(CM=BM=\dfrac{BC}{2}\)(M là trung điểm của BC)
nên AM=CM=BM(3)
Từ (1), (2) và (3) suy ra AM=AF=CF=CM=BM
Xét tứ giác AMCF có AM=CM=CF=FA(cmt)
nên AMCF là hình thoi(Dấu hiệu nhận biết hình thoi)
b)
Sửa đề: Tìm điều kiện của ΔABC để tứ giác AMCF là hình vuông
Hình thoi AMCF trở thành hình vuông khi \(\widehat{AMC}=90^0\)
hay \(AM\perp BC\)
Xét ΔABC có
AM là đường cao ứng với cạnh BC(\(AM\perp BC\))
AM là đường trung tuyến ứng với cạnh BC(M là trung điểm của BC)
Do đó: ΔABC cân tại A(Định lí tam giác cân)
hay AB=AC
Vậy: Khi ΔABC có thêm điều kiện AB=AC thì AMCF trở thành hình vuông
c)
Ta có: MD\(\perp\)AB(gt)
AC\(\perp\)AB(ΔABC vuông tại A)
Do đó: MD//AC(Định lí 1 từ vuông góc tới song song)
Xét ΔABC có
M là trung điểm của BC(gt)
MD//AC(cmt)
Do đó: D là trung điểm của AB(Định lí 1 đường trung bình của tam giác)
Xét ΔABC có
M là trung điểm của BC(gt)
D là trung điểm của AB(cmt)
Do đó: MD là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
nên \(MD=\dfrac{AC}{2}\)(Định lí 2 đường trung bình của tam giác)(1)
Ta có: \(ME\perp AC\)(gt)
\(AB\perp AC\)(ΔABC vuông tại A)
Do đó: ME//AB(Định lí 1 từ vuông góc tới song song)
Xét ΔABC có
M là trung điểm của BC(gt)
ME//AB(cmt)
Do đó: E là trung điểm của AC(Định lí 1 đường trung bình của tam giác)
nên \(CE=\dfrac{AC}{2}\)(2)
Từ (1) và (2) suy ra MD=CE
Xét tứ giác CMDE có
MD//CE(MD//AC)
MD=CE(cmt)
Do đó: CMDE là hình bình hành(Dấu hiệu nhận biết hình bình hành)
nên Hai đường chéo CD và EM cắt nhau tại trung điểm của mỗi đường(Định lí hình bình hành)
mà I là trung điểm của EM(gt)
nên I là trung điểm của CD(đpcm)
Cho ΔABC vuông tại A. Vẽ tia phân giác của góc ABC cắt cạnh AC tại H. Từ H vẽ HM ⊥ BC tại M. Gọi N là giao điểm của tia BA và tia MH.
a) Chứng minh: ΔABH = ΔMBH
b) Chứng minh: ΔAHN = ΔMHC
c) Chứng minh: BH vuông góc NC
d) Gọi K là trung điểm của cạnh NC. Chứng minh ba điểm B, H, K thẳng hàng.
a: Xét ΔBAH vuông tại A và ΔBMH vuông tại M có
BH chung
góc ABH=góc MBH
=>ΔBAH=ΔBMH
b: Xét ΔHAN vuông tại A và ΔHMC vuông tại M có
HA=HM
góc AHN=góc MHC
=>ΔHAN=ΔHMC
c: BN=BC
HN=HC
=>BH là trung trực của NC
=>BH vuông góc NC
c: BH là trung trực của NC
K là trung điểm của NC
=>B,H,K thẳng hàng
Cho ΔABC vuông tại A (AB < AC), đường cao AH. Trên cạnh AC lấy điểm D sao cho AD = AB. Gọi O là trung điểm của BD. . Vẽ (O) đường kính BD cắt cạnh BC tại điểm thứ hai K.
a, C/m: A thuộc đường tròn (O)
b, C/m: \(\widehat{AKB}=\widehat{ADB}\)
c, C/m: CK.CB = CD.CA
d, Tính \(\widehat{AHO}\)
a) Ta có: ΔABD vuông tại A(gt)
nên A nằm trên đường tròn đường kính BD(Định lí quỹ tích cung chứa góc)
mà BD là đường kính của (O)
nên A\(\in\)(O)(Đpcm)
b) Xét (O) có
\(\widehat{AKB}\) là góc nội tiếp chắn cung AB
\(\widehat{ADB}\) là góc nội tiếp chắn cung AB
Do đó: \(\widehat{AKB}=\widehat{ADB}\)(Hệ quả góc nội tiếp)
Cho ΔABC vuông tại A, có AB = 9cm, BC = 15 cm, AC=12 cm.
a) so sánh các góc của ΔABC
b) trên tia đối của AB lấy điểm D sao cho A là trung điểm của đoạn thẳng BD. Chừng minh ΔABC = ΔADC
c) E là trung điểm cạnh CD,BE cắt AC ở I. Chứng minh DI đi qua trung điểm cạnh BC
a: AB<AC<BC
=>góc C<góc B<góc A
b: Xet ΔABC có
BC^2=AB^2+AC^2
=>ΔBCA vuông tại A
Xet ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD
=>ΔCAB=ΔCAD
c: Xét ΔCBD có
CA,BE là trung tuyến
CA cắt BE tại I
=>I là trọng tâm
=>DI đi qua trung điểm của BC
Cho ΔABC vuông tại H, gọi M,N lần lượt là trung điểm của cạnh BC,AC. D là điểm đối xứng với N qua M.
a) CMR: tứ giác BDCN là hình bình hành.
b) CMR; AD=BN.
c) Tia AM cắt CD ở E. CMR: CE=2DE.
Hình bạn tự vẽ nha
a) CMR Tứ giác BDCN là hình bình hành
Vì D đối xứng N qua M (gt) => M là trung điểm của DM (đn)
Xét tứ giác BDCN có
M là trung điểm BC (gt)
M là trung điểm DM (cmt)
=> Tứ giác BDCN là hbh (dhnb hbh)
b) CMR AD=BN
Vì BDCN là hbh( cmt) => BD//NC => BD//AN (1) và BD=NC
mà NC=AN (N là trung điểm AC)
=> BD=NC (bắc cầu) (2)
Mà BAC=90 (gt) (3)
Từ (1) và (2), (3)=> BDNA hcn (dhnb hcn)=> AD=BN (t/c đường chéo hcn)
c) CMR EC=2DE
Xét tam giác ACE có
N là trung điểm AC (gt)
FN//EC (BN//DC)
=> F là trung điểm của AE ( định lý đường trung bình)
mà N là trung điểm của AC (gt)
=> FN là đường TB của tam giác AEC ( đn)
=> FN= 1/2 EC (1)
Xét tam giác FNM=tam giác EMD (cgc)
=> DE=FN ( 2 góc t/ư)(2)
Từ (1) và (2) => DE=1/2 EC ( bắc cầu)
Đề bài sai thì làm thế nào?
Tại sao tam giác ABC vuông tại H?Vuông tại A đúng ko?