Cho (O,12cm); trên (O) lấy các điểm A,B,C,D theo thứ tự đó sao cho góc AOB=90 độ, góc BOC=60 độ, góc COD=120 độ a)Tính chu vi tứ giác ABCD b)Chứng minh ABCD là hình thang cân

Những câu hỏi liên quan
Cho ΔABC cân tại B có góc ABC=1200,AB=12cm và nội tiếp (O).Bán kính của (O) bằng
A.10cm B.9cm C.8cm D.12cm
\(\dfrac{BC}{\sin A}=\dfrac{AC}{\sin B}=\dfrac{AB}{\sin C}=2R\)
\(R=\dfrac{AB}{2.\sin C}=\dfrac{12}{2.\sin30}=12cm\)
\(\Rightarrow\) Chọn D
Đúng 1
Bình luận (0)
Cho ΔABC cân tại B có góc ABC=1200,AB=12cm và nội tiếp (O).Bán kính của (O) bằng
A.10cm B.9cm C.8cm D.12cm
Đúng 0
Bình luận (0)
cho ( O;10cm), một dây của đường tròn (O) có độ dài bằng 12cm. khoảng cách từ tâm O đến dây này là ?
A. 12cm B. 8cm C. 6cm D. 10cm
Đáp án: B. 8cm
Lời giải:
Gọi dây trên là dây AB. Hạ OH\(\perp\)AB = {H} (cd)
Xét (O) 1 phần đường kính OH: OH\(\perp\)AB = {H} (cd)
=> H là trung điểm AB (đl) => HA = HB = AB: 2 = 12:2 = 6 (cm)
OH\(\perp\)AB = {H} (cd) => \(\Delta\)OHB vuông tại H (đn)
=> OH\(^2\)+ HB\(^2\)= OB\(^2\)(Đl Py-ta-go)
T/s: OH\(^2\)+ 6\(^{^2}\)= R\(^2\)
<=> OH\(^2\)+36 = 10\(^2\)=100
<=> OH\(^2\)= 64 => OH = 8 (cm)
\(^2\)
Câu1:Cho tam giác ABC,góc A bằng 90°,có cạnh AB 6,tgB4/3.Tính cạnh BC.
Câu2:Cho(O;12cm),một dây cũng của đường tròn tâm O có độ dài bằng bán kính.Tính khoảng cách từ tâm đến dây cũng.
Câu3:Hai đường tròn (O;R)và O;R)d.Biết R12cm,R7cm,d4 thì vị trí tương đối của 2 đường tròn là?
Câu4:Cho hàm số y(2m-1)x+3
a)Tìm m.để HS đi qua điểm A(2;5)
b)Vẽ đths vs m tìm đc ở câu a
Câu5:Cho(O;R),1 đường thẳng d cắt đường tròn (O) tại C,D,lấy điểm M trên đường thẳng d sao cho D nằm giữa C và M.Qua M vẽ tiếp tuyế...
Đọc tiếp
Câu1:Cho tam giác ABC,góc A bằng 90°,có cạnh AB =6,tgB=4/3.Tính cạnh BC. Câu2:Cho(O;12cm),một dây cũng của đường tròn tâm O có độ dài bằng bán kính.Tính khoảng cách từ tâm đến dây cũng. Câu3:Hai đường tròn (O;R)và O';R')=d.Biết R=12cm,R'=7cm,d=4 thì vị trí tương đối của 2 đường tròn là? Câu4:Cho hàm số y=(2m-1)x+3 a)Tìm m.để HS đi qua điểm A(2;5) b)Vẽ đths vs m tìm đc ở câu a Câu5:Cho(O;R),1 đường thẳng d cắt đường tròn (O) tại C,D,lấy điểm M trên đường thẳng d sao cho D nằm giữa C và M.Qua M vẽ tiếp tuyến MA,MB với đường tròn.Gọi H là trung điểm của CD,OM cắt AB tại E.CMR a)AB vuông góc với OM b)Tích OE.OM ko đổi c)Khi M di chuyển trên đường thẳng d thì đường thẳng AB đi qua 1 điểm cố định. (Mọi người giúp e vs ạ)
Câu 1:
Xét ΔABC vuông tại A có
\(tanB=\dfrac{AC}{AB}\)
=>\(\dfrac{AC}{6}=\dfrac{4}{3}\)
=>\(AC=\dfrac{4}{3}\cdot6=8\left(cm\right)\)
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Câu 4:
a: Thay x=2 và y=5 vào y=(2m-1)x+3, ta được:
2(2m-1)+3=5
=>2(2m-1)=2
=>2m-1=1
=>2m=2
=>\(m=\dfrac{2}{2}=1\)
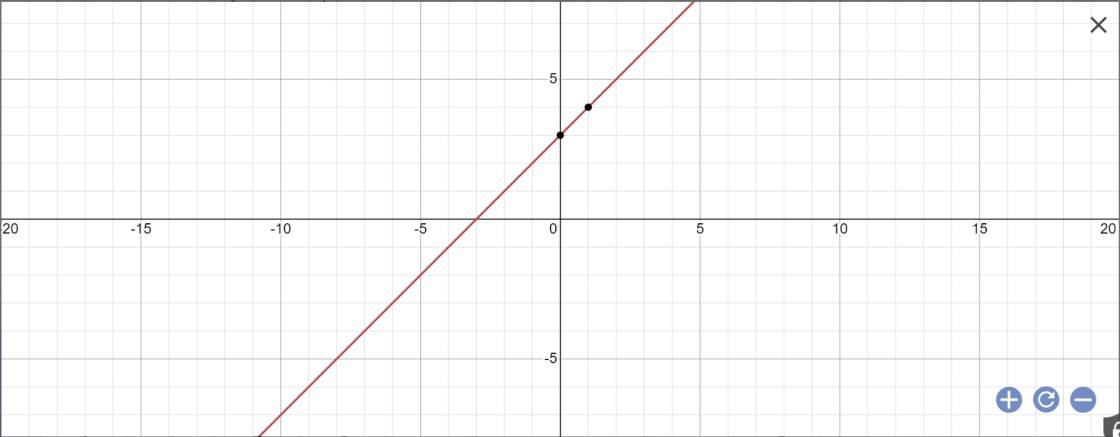
b: Khi m=1 thì \(y=\left(2\cdot1-1\right)x+3=x+3\)
Đúng 1
Bình luận (0)
Cho (O; 20cm) và dây AB bằng 24cm. Khoảng cách từ O đến dây AB bằng:a.156−−−√cmb.16cmc.6cmd.12cm
Đọc tiếp
Cho (O; 20cm) và dây AB bằng 24cm. Khoảng cách từ O đến dây AB bằng:a.156−−−√cmb.16cmc.6cmd.12cm
Cho đoạn thẳng AB=12cm. Gọi O là trung điểm của AB. Độ dài OB là:
Xem thêm câu trả lời
Bài 1: Cho đường tròn tâm O, bán kính 10cm và dây AB = 12cm. Tính khoảng cách từ tâm O đến dây AB
Lời giải:
Gọi dây trên là dây AB. Hạ OH⊥⊥AB = {H} (cd)
Xét (O) 1 phần đường kính OH: OH⊥⊥AB = {H} (cd)
=> H là trung điểm AB (đl) => HA = HB = AB: 2 = 12:2 = 6 (cm)
OH⊥⊥AB = {H} (cd) => ΔΔOHB vuông tại H (đn)
=> OH22+ HB22= OB22(Đl Py-ta-go)
T/s: OH22+ 622= R22
<=> OH22+36 = 1022=100
<=> OH22= 64 => OH = 8 (cm)
Gọi H là chân đường cao kẻ từ O
=> H là trung điểm AB
=> AH = AB/2 = 12/2 = 6 cm
Theo định lí Pytago cho tam giác AOH vuông tại H
\(AO^2=OH^2+AH^2\Rightarrow OH^2=AO^2-AH^2=100-36=64\Rightarrow OH=8\)cm
cho đường tròn (O;10cm) và dây AB = 12cm. Gọi OH là khoảng cách từ tâm O đến dây AB. Khi đó, độ dài OH bằng?
Xét (O) có
OH là một phần đường kính
AB là dây
OH\(\perp\)AB tại H
Do đó: H là trung điểm của AB
=>AH=AB/2=6(cm)
Xét ΔOHA vuông tại H có
\(OA^2=OH^2+AH^2\)
hay OH=8cm
Đúng 1
Bình luận (0)
cho đường tròn (O;13cm), dây AB cách tâm O một khoảng bằng 5cm có đô dài là :
A. 3cm B.6cm C.24cm D.12cm
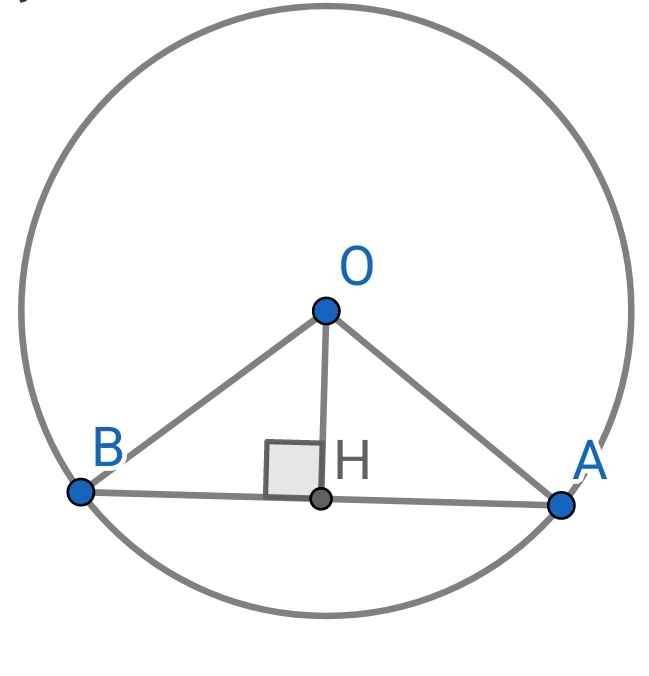
∆OBH vuông tại H
⇒ OB² = OH² + BH² (Pytago)
⇒ BH² = OB² - OH²
= 13² - 5²
= 144
⇒ BH = 12 (cm)
⇒ AB = 2BH = 2.12 = 24 (cm)
Chọn C
Đúng 0
Bình luận (0)
Cho (O;R) và (O';R') cắt nhau tại A, B. Đoạn nối tâm OO' cắt (O) tại C cắt (O') tại D. Biết AB = 24cm, CD = 12cm. Tính bán kính R.
Cho (O) bán kính 10cm. Biết dây AB=12cm. Gọi M là trung điểm của AB. Tính OM.
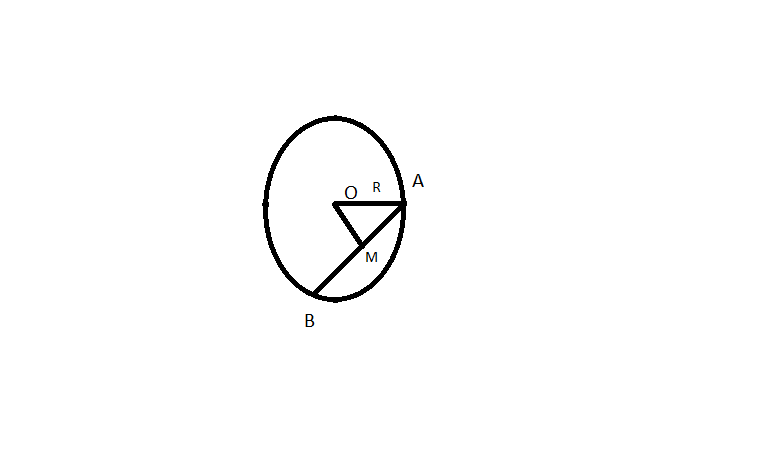
M là trung điểm AB\(\Rightarrow\) AM=6cm
OA=R=10cm
\(\Rightarrow OM=\sqrt{OA^2+AM^2}=\sqrt{10^2+6^2=}2\sqrt{34}cm\)
Đúng 1
Bình luận (0)




























