Cho góc nhọn xOy, vẽ tia phân giác Oz. Trên Ox lấy điểm A và trên Oy lấy điểm B sao cho OA=OB; lấy điểm M bất kì trên Oz. Chứng minh:
a) MA=MB
b) OM⊥ AB
cho góc nhọn xOy và tia phân giác Oz của góc đó .Trên tia Ox lấy điểm a ,trên tia Oy lấy điểm b sao cho oa=ob . trên tia Oz lấy điểm I bất kì chứng minh a) tam giác AOI = tam giác BOI
B) AB VUÔNG GÓC OI
Ta có hình vẽ:
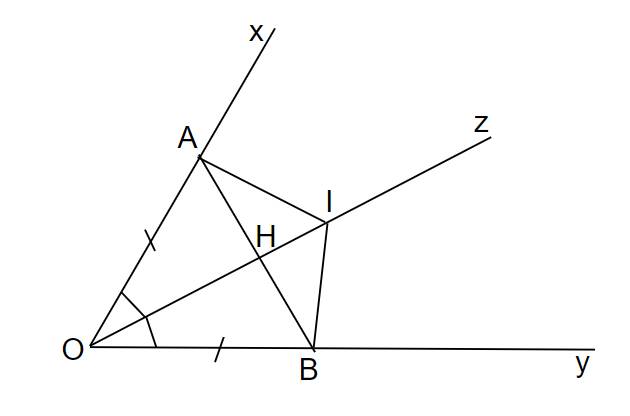
a) Vì Oz là phân giác của xOy nên
Xét Δ AOI và Δ BOI có:
OA = OB (gt)
AOI = BOI (cmt)
OI là cạnh chung
Do đó, Δ AOI = Δ BOI (c.g.c) (đpcm)
b) Xét Δ AOH và Δ BOH có:
OA = OB (gt)
AOH = BOH (câu a)
OH là cạnh chung
Do đó, Δ AOH = Δ BOH (c.g.c)
=> AHO = BHO (2 góc tương ứng)
Mà AHO + BHO = 180o (kề bù) nên AHO = BHO = 90o
=>
1. Cho góc xOy nhọn và tia phân giác Oz. Lấy điểm A trên tia Ox, điểm B trên tia Oy sao cho OA = OB. Lấy điểm I thuộc tia Oz. Chứng minh:
a)△AOI=△BOI
b) AB ⊥ OI
a: Xét ΔOAI và ΔOBI có
OA=OB
\(\widehat{AOI}=\widehat{BOI}\)
OI chung
Do đó: ΔOAI=ΔOBI
\(a,\left\{{}\begin{matrix}OA=OB\\\widehat{AOI}=\widehat{BOI}\\OI\text{ chung}\end{matrix}\right.\Rightarrow\Delta AOI=\Delta BOI\left(c.g.c\right)\\ b,\text{Gọi }AB\cap OI=\left\{H\right\}\\ \left\{{}\begin{matrix}OA=OB\\\widehat{AOI}=\widehat{BOI}\\OH\text{ chung}\end{matrix}\right.\Rightarrow\Delta AOH=\Delta BOH\left(c.g.c\right)\\ \Rightarrow\widehat{AHO}=\widehat{BHO}\\ \text{Mà }\widehat{AHO}+\widehat{BHO}=180^0\\ \Rightarrow\widehat{AHO}=\widehat{BHO}=90^0\\ \Rightarrow OI\bot AB\)
Cho góc nhọn xOy và Oz là tia phân giác của góc đó. Trên tia Ox lấy điểm A và trên tia Oy lấy điểm B sao cho OA=OB. Gọi C là một điểm bất kì trên tia Oz
Chọn câu sai
A. AC = OB
B. AC = BC
C. O A C ^ = O B C ^
D. CO là tia phân giác của B C A ^
a: Xét ΔOAC và ΔOBC có
OA=OB
\(\widehat{AOC}=\widehat{BOC}\)'
OC chung
Do đó: ΔOAC=ΔOBC
=>AC=BC và \(\widehat{OAC}=\widehat{OBC}\)
\(\widehat{OAC}+\widehat{xAC}=180^0\)(hai góc kề bù)
\(\widehat{OBC}+\widehat{yBC}=180^0\)(hai góc kề bù)
mà \(\widehat{OAC}=\widehat{OBC}\)
nên \(\widehat{xAC}=\widehat{yBC}\)
b: OA=OB
=>O nằm trên đường trung trực của AB(1)
CA=CB
=>C nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OC là đường trung trực của AB
=>OC\(\perp\)AB
=>Oz\(\perp\)AB
4. Cho góc nhọn xOy và tia phân giác Oz của góc đó. Trên Ox, lấy điểm A, trên Oy lấy điểm B sao cho OA = OB. Trên tia Oz, lấy điểm I bất kì. Chứng minh:
a. Δ AOI = Δ BOI.
b. AB ⊥ OI.
a: Xét ΔOAI và ΔOBI có
OA=OB
\(\widehat{AOI}=\widehat{BOI}\)
OI chung
Do đó: ΔOAI=ΔOBI
Cho góc nhọn xOy và tia phân giác Oz của góc đó . trên tia ox lẤY A TRÊN TIA OY LẤY B SAO CHO Oa = ob trên tIA Oz lấy điểm Ý chung MINH TAM GIÁc aoy = tam giác BỞI , AB vuông góC VỚI OY
Bài 5: Cho góc nhọn xOy. Vẽ tia phân giác Oz, trên tia Ox, Oy lần lượt lấy 2 điểm A và B sao cho OA = OB. Gọi I là giao điểm của AB với Oz
a/ Trên tia Oz lấy điểm E sao cho OI = IE. Chứng minh: BE//OA ; b/Chứng minh: AB ![]() OE
OE
a: Xét tứ giác BOAE có
I là trung điểm của BA
I là trung điểm của OE
Do đó: BOAE là hình bình hành
Suy ra: BE//OA
cho góc xOy nhọn và tia phân giác của góc xOy. Trên tia Ox lấy A , Oy lấy B sao cho OA=OB. Trên tia Oz lấy điểm M tùy ý
chứng minh AOB là tam giác cân
Giúp mình giải với