Cho tg ABC có góc A = 110o; góc C = 30o. Vẽ ra ngoài tg DAC có góc DAC = góc DCA = 50o
C/M tg ABD cân.
Giúp mình nhé, mình cần gấp lắm.
Những câu hỏi liên quan
cho △ABC có góc A=110o, I là trung điểm của BC. Trên tia đối của tia IA lấy K sao cho IK=IA
a, Chứng minh △AIB=△KIC
b, Tính góc ACK
a) Xét \(\Delta AIBvà\Delta KICcó\)
AI=KI( giả thiết)
\(\widehat{AIB}=\widehat{KIC}\) (2 góc đối đỉnh)
IB=IC(vì I là trung điểm của BC )
\(\Rightarrow\Delta AIB=\Delta KIC\left(c-g-c\right)\)
vậy \(\Delta AIB=\Delta KIC\)
b)vậy \(\Delta AIB=\Delta KIC\)(chứng minh câu a )
\(\Rightarrow\widehat{KCI}=\widehat{ABI}\) ( 2 góc tương ứng )
hay \(\widehat{KCB}=\widehat{ABC}\) mà 2 góc này là 2 góc so le trong của đường thẳng CB cắt 2 đường thẳng CK và AB
\(\Rightarrow CK//AB\)
\(\Rightarrow\widehat{AC}K+\widehat{BAC}=180độ\) (2 góc trong cùng phía )
\(\Rightarrow\widehat{ACK}+110độ=180độ\)
\(\Rightarrow\widehat{ACK}=180độ-110độ=70độ\)
Vậy\(\widehat{ACK}=70độ\)
Đúng 1
Bình luận (0)
a) Xét \(\Delta AIBvà\Delta KICcó\)
AI=KI( giả thiết)
\(\widehat{AIB}=\widehat{KIC}\) (2 góc đối đỉnh)
IB=IC(vì I là trung điểm của BC )
\(\Rightarrow\Delta AIB=\Delta KIC\left(c-g-c\right)\)
vậy \(\Delta AIB=\Delta KIC\)
b)vậy \(\Delta AIB=\Delta KIC\)(chứng minh câu a )
\(\Rightarrow\widehat{KCI}=\widehat{ABI}\) ( 2 góc tương ứng )
hay \(\widehat{KCB}=\widehat{ABC}\) mà 2 góc này là 2 góc so le trong của đường thẳng CB cắt 2 đường thẳng CK và AB
\(\Rightarrow CK//AB\)
\(\Rightarrow\widehat{AC}K+\widehat{BAC}=180độ\) (2 góc trong cùng phía )
\(\Rightarrow\widehat{ACK}+110độ=180độ\)
\(\Rightarrow\widehat{ACK}=180độ-110độ=70độ\)
Vậy\(\widehat{ACK}=70độ\)
Đúng 0
Bình luận (0)
21 tháng 6 2021 lúc 10:30
b1: cho tg abc vg tại a, có ab= 5cm, sin góc c= 1/2
a) tính góc C, góc B
b) tính các cạnh còn lại ở tg vg abc và đg cao ah
B2: cho tg abc vg tại a có tan góc B= 5/12 và ab= 30cm
a, tính bc, ac, đg cao ah
b,tính cotan góc cah, cotan góc bah
Tam giác ABC có ∠A = 40o. Các tia phân giác của các góc B và C cắt nhau ở I.
Góc BIC bằng:
(A) 40o;
(B) 70o;
(C) 110o;
(D) 140o.
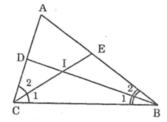
Ta có:
+ Trong ΔBIC có ∠BIC = 180º - (∠B1 + ∠C1) (1)
+ BI, CI là phân giác của ∠ABC và ∠BCA nên:
∠B1 = 1/2. ∠BAC; ∠C1 = 1/2. ∠ACB
⇒ ∠B1 + ∠C1 = 1/2. (∠BAC + ∠BCA) (2)
+ Trong ΔABC có: ∠BAC + ∠BCA = 180 - ∠A =140º (3).
Từ (1), (2) và (3) suy ra ∠BIC = 180º - 1/2.140º = 110º
Chọn đáp án C
Đúng 0
Bình luận (0)
cho tg ABC có góc A<90 độ. Vẽ ra ngoài tg ABC các tg ABD và ACE vuông cân tại A. CM BE=CD và BE vuông góc với CD
Bài 1: cho tam giác ABC cân tại A có góc A= 20 độ. Trên AB láy M sao cho AM=BC. Tính góc AMC (gợi ý: vẽ tam giác BDC đều nằm trong tam giác ABC)
bài 2: cho tg ABC cân tại A. góc A=40 độ. kẻ AH vuông với BC. lấy E và F thuộc AH và AC sao cho góc ABC = góc FBC = 30 độ. Tính góc AEF
bài 3:cho tg ABC có góc B= góc C=45 độ. điểm E nằm trong tg ABC sao cho góc EAC= góc ECA= 15 độ. Tính góc BEA.
23 tháng 6 2021 lúc 16:43
a) cho tg abc vg tại a có tan góc b=2.hãy tính các tỉ số lượng giác của góc c b) cho tg abc vg tại a, có sin góc b = căn 3 phần 2. tính các tỉ số lượng giác góc b
23 tháng 6 2021 lúc 13:33
a) cho tg abc vg tại a có tan góc b=2.hãy tính các tỉ số lượng giác của góc c
b) cho tg abc vg tại a, có sin góc b = căn 3 phần 2. tính các tỉ số lượng giác góc b
Cho hình vẽ sau: Biết
A
D
∥
B
C
,
B
A
D
^
110
o
, AD
⊥
DC. Số đo góc ABC A. 90
°
B. 100
°
C. 80
°
D. 70
°
Đọc tiếp
Cho hình vẽ sau:
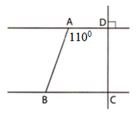
Biết A D ∥ B C , B A D ^ = 110 o , AD ⊥ DC. Số đo góc ABC
A. 90 °
B. 100 °
C. 80 °
D. 70 °
Cho tg ABC cân tại A, có góc A < 90*, kẻ BH vuông góc với AC, CK vuông góc với AC. gọi O là giao điểm của BH và CK.
a, cm tg ABH= tg ACH.
b,tg OBC cân
c, tg OBK=tgOCK
a)Vì ABC cân tại A (gt) => AB = AC (TC Tg cân)
BH vg góc AC (gt) => ^AHB=^CHB = 90o
CK vg góc AB (gt) => ^AKC=^BKC = 90o
Xét tg ABH và tg ACK:
^AHB = ^AKC (= 90)
^A chung
AB = AC (cmt)
=> tg ABH = tg ACK (ch - gn)
b) Xét tg BKC và tg CHB :
^BKC = ^CHB (=90)
BC chung
^B = ^C (tg ABC cân tại A)
=> tg BKC và tg CHB (ch - gn)
=> ^KCB = ^HBC (2 góc tương ứng)
hay ^OBC = ^OCB
=> tg OBC cân tại O (đpcm)
c) tg BKC và tg CHB (cmt) => BK = CH (2 cạnh tương ứng)
Ta có: ^B = ^ABH + ^CBH
^C = ^ACK + ^BCK
Mà ^B = ^C (tg ABC cân tại A); ^CBH = ^BCK(cmt)
=> ^ABH = ^ACK
Xét tg OBK và tgOCK:
^BKO = ^CHO (=90)
BK = CH (cmt)
^KBO = ^HCO (^ABH = ^ACK)
=> tg OBK = tg OCK (gcg)
Đúng 1
Bình luận (0)
a) Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC(ΔABC cân tại A)
\(\widehat{BAH}\) chung
Do đó: ΔABH=ΔACK(cạnh huyền-góc nhọn)
b) Ta có: ΔABH=ΔACK(cmt)
nên \(\widehat{ABH}=\widehat{ACK}\)(hai góc tương ứng)
Ta có: \(\widehat{ABH}+\widehat{CBH}=\widehat{ABC}\)(tia BH nằm giữa hai tia BA,BC)
\(\widehat{ACK}+\widehat{BCK}=\widehat{ACB}\)(tia CK nằm giữa hai tia CA,CB)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy trong ΔABC cân tại A)
và \(\widehat{ABH}=\widehat{ACK}\)(cmt)
nên \(\widehat{CBH}=\widehat{BCK}\)
hay \(\widehat{OBC}=\widehat{OCB}\)
Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)(cmt)
nên ΔOBC cân tại O(Định lí đảo của tam giác cân)
c)
Sửa đề: ΔOBK=ΔOCH
Xét ΔOBK vuông tại K và ΔOCH vuông tại H có
OB=OC(ΔOBC cân tại O)
\(\widehat{OBK}=\widehat{OCH}\)(cmt)
Do đó: ΔOBK=ΔOCH(cạnh huyền-góc nhọn)
Đúng 0
Bình luận (0)