Cho hình thang ABCD có M, N theo thứ tự là trung điểm của AD; AC; cạnh MN cắt BC tại P. Biết CD = 10cm và NP = 3cm. Tính AB
A. 5cm
B. 6cm
C. 7cm
D. 6,5 cm
Những câu hỏi liên quan
Cho hình thang vuông ABCD có góc A= góc D=90 có AB=3,AD=8,CD=5. M,N theo thứ tự là trung điểm BC,AD. Gọi K là hình chiếu của M trên CD . Chứng minh MNDK là hình vuông
Cho hình thang ABCD (AB//CD.Gọi E,F theo thứ tự là trung điểm của AB,CD. Gọi O là trung điểm của EF. Qua O kẻ đường thẳng song song với AB, cắt AD và BC theo thứ tự ở M và N
a, Tứ giác EMFN là hình gì ? Vì sao?
b, Hình thang ABCD có thêm điều kiện gì thì EMFN là hình thoi?
c, Hình thang ABCD có thêm điều kiện gì thì EMFN là hình vuông?
a) Ta có: AB//CD(gt)
mà E∈AB và F∈CD
nên AE//DF và EB//FC
Xét tứ giác AEFD có AE//DF(cmt)
nên AEFD là hình thang có hai đáy là AE và DF(Định nghĩa hình thang)
Hình thang AEFD(AE//DF) có
O là trung điểm của EF(gt)
OM//AE//DF(MN//AB//DC, E∈AB, O∈MN, F∈DC)
Do đó: M là trung điểm của AD(Định lí 3 về đường trung bình của hình thang)
Xét tứ giác BEFC có BE//FC(cmt)
nên BEFC là hình thang có hai đáy là BE và FC(Định nghĩa hình thang)
Hình thang BEFC(BE//FC) có
O là trung điểm của EF(gt)
ON//EB//FC(MN//AB//DC, E∈AB, O∈MN, F∈CD)
Do đó: N là trung điểm của BC(Định lí 3 về đường trung bình của hình thang)
Xét ΔABD có
M là trung điểm của AD(cmt)
E là trung điểm của AB(gt)
Do đó: ME là đường trung bình của ΔABD(Định nghĩa đường trung bình của tam giác)
⇒ME//BD và NF=BD2NF=BD2(Định lí 2 về đường trung bình của tam giác)(2)
Từ (1) và (2) suy ra ME//NF và ME=NF
Xét tứ giác EMFN có ME//NF(cmt) và ME=NF(cmt)
nên EMFN là hình bình hành(Dấu hiệu nhận biết hình bình hành)
b) Xét ΔBAC có
E là trung điểm của AB(gt)
N là trung điểm của BC(cmt)
Do đó: EN là đường trung bình của ΔBAC(Định nghĩa đường trung bình của tam giác)
⇒EN//AC và EM=BD2EM=BD2(cmt) và
Đúng 0
Bình luận (0)
13 tháng 12 2020 lúc 10:25
Cho hình thang ABCD(AB//CD).Gọi E,F theo thứ tự là trung điểm của AB,CD.Qua trung điểm O của EF,kẻ đường thẳng song song với AB cắt AD và BC tại M,N.
a)EMFN là hình gì?Vì sao?
b)Hình thang ABCD có thêm điều kiện gì thì EMFN là hình thoi?
c)Hình thang ABCD có thêm điều kiện gì thì EMFN là hình vuông?
MỌI NGƯỜI GIÚP MÌNH VỚI Ạ.CẢM ƠN NHÌU NHÌU:333
a) Ta có: AB//CD(gt)
mà E∈AB và F∈CD
nên AE//DF và EB//FC
Xét tứ giác AEFD có AE//DF(cmt)
nên AEFD là hình thang có hai đáy là AE và DF(Định nghĩa hình thang)
Hình thang AEFD(AE//DF) có
O là trung điểm của EF(gt)
OM//AE//DF(MN//AB//DC, E∈AB, O∈MN, F∈DC)
Do đó: M là trung điểm của AD(Định lí 3 về đường trung bình của hình thang)
Xét tứ giác BEFC có BE//FC(cmt)
nên BEFC là hình thang có hai đáy là BE và FC(Định nghĩa hình thang)
Hình thang BEFC(BE//FC) có
O là trung điểm của EF(gt)
ON//EB//FC(MN//AB//DC, E∈AB, O∈MN, F∈CD)
Do đó: N là trung điểm của BC(Định lí 3 về đường trung bình của hình thang)
Xét ΔABD có
M là trung điểm của AD(cmt)
E là trung điểm của AB(gt)
Do đó: ME là đường trung bình của ΔABD(Định nghĩa đường trung bình của tam giác)
⇒ME//BD và \(ME=\dfrac{BD}{2}\)(Định lí 2 về đường trung bình của tam giác)(1)
Xét ΔBDC có
N là trung điểm của BC(cmt)
F là trung điểm của CD(gt)
Do đó: NF là đường trung bình của ΔBDC(Định nghĩa đường trung bình của tam giác)
⇒NF//BD và \(NF=\dfrac{BD}{2}\)(Định lí 2 về đường trung bình của tam giác)(2)
Từ (1) và (2) suy ra ME//NF và ME=NF
Xét tứ giác EMFN có ME//NF(cmt) và ME=NF(cmt)
nên EMFN là hình bình hành(Dấu hiệu nhận biết hình bình hành)
b) Xét ΔBAC có
E là trung điểm của AB(gt)
N là trung điểm của BC(cmt)
Do đó: EN là đường trung bình của ΔBAC(Định nghĩa đường trung bình của tam giác)
⇒EN//AC và \(EN=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)
Hình bình hành EMFN trở thành hình thoi khi EM=EN
mà \(EM=\dfrac{BD}{2}\)(cmt) và \(EN=\dfrac{AC}{2}\)(cmt)
nên BD=AC
Vậy: Khi hình thang ABCD có thêm điều kiện BD=AC thì EMFN là hình thoi
Đúng 3
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B. Biết
A
B
B
C
a
,
A
D
2
a
,
S
A
3
a
2
2
,
S
A
⊥
A
B
C
D
....
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B. Biết A B = B C = a , A D = 2 a , S A = 3 a 2 2 , S A ⊥ A B C D . M, N theo thứ tự là trung điểm của SB, SA. Khoảng cách từ N đến mặt phẳng (MCD) bằng:
A. a 3
B. a 4
C. 4 a 3
D. 3 a 4
Chọn B.
Phương pháp:
Gắn hệ trục tọa độ.
Cách giải:
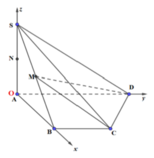
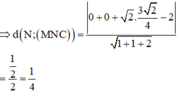
Vây, khoảng cách từ N đến mặt phẳng (MCD) bằng: 1 4 a
Đúng 0
Bình luận (0)
Cho hình thang ABCD có hai đáy AB và CD Gọi G,H theo thứ tự là trung điểm của AD và BC .Chứng minh rằng G, H là đường trung bình của hình thang ABCD.
Xét hình thang ABCD có
G là trung điểm của AD
H là trung điểm của BC
Do đó: GH là đường trung bình của hình thang ABCD
Đúng 0
Bình luận (0)
Bài 7: Cho hình thang vuông ABCD có góc A bằng góc D và cùng bằng 90. AB = 3cm, AD = 8cm. CD = 5cm. Gọi M, N theo thứ tự là trung điểm của BC, AD. Gọi K là hình chiếu của M trên CD. Chứng minh MNDK là hình vuông
cho hình thang ABCD (AB//CD).Gọi E là trung điểm của AB, F là trung điểm của CD ,O là trung điểm của EF . Qua O kẻ đường thẳng song song với CD , cắt AD và BC theo thứ tự ở M và N .
a) Chứng minh rằng M là trung điểm của AD , N là trung điểm của BC
b) Chứng minh rằng OM=ON
c)Tứ giác EMFN là hình gì ?
GIÚP MÌNH NHÉ MÌNH CẦN GẤP
cho hình thang ABCD có E,F theo thứ tự là trung điểm của AD,BC.Cm EF ≤ AB+DC/2
Tham khảo đây nha:
https://hoidap247.com/cau-hoi/1107494
Đúng 1
Bình luận (0)
cho hình thang ABCD,M là trung điểm của AD,N là trung điểm của BC.gọi I,K theo thứ tự là giao điểm của MN với BD,AC.cho biết AB=6cm,CD=14cm.tính các độ độ dài MI,IK,KN.
