Cho tứ diện ABCD có DA vuông góc với (ABC) và AD = a, AC = 2a; cạnh BC vuông góc với cạnh AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện ABCD.
A. r = a 5
B. r = a 3 2
C. r = a
D. r = a 5 2
Cho tứ diện ABCD có DA vuông góc với mặt phẳng (ABC) và AD = a, AC = 2a. cạnh BC vuông góc với AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện ABCD.
A. r = a 5
B. r = a 3 2
C. r = a
D. r = a 5 2
Cho tứ diện A B C D có DA vuông góc với mặt phẳng ( A B C ) và A D = a , A C = 2 a , cạnh BC vuông góc với AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện A B C D .
![]()
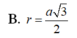
![]()
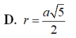
Cho tứ diện ABCD có cạnh AB,AC,AD đôi một vuông góc. Biết rằng A B = A C = 2 a và góc tạo bởi hai mặt phẳng (DCB) và (ABC) bằng 60 0 . Tính thể tích khối tứ diện ABCD.
A. 2 6 a 3 3
B. 4 6 a 3 3
C. 2 6 a 3
D. 4 6 a 3
Cho tứ diện ABCD có cạnh DA vuông góc với mặt phẳng (ABC) và AB=3cm, AC=4cm, A D = 6 c m , BC=5cm. Khoảng cách từ A đến mặt phẳng (BCD) bằng
A. 12 5 c m .
B. 12 7 c m .
C. 6 c m
D. 6 10 c m .
Cho tứ diện ABCD có cạnh DA vuông góc với mặt phẳng (ABC) và AB=3cm, AC=4cm, AD= 6 CM, BC=5cm. Khoảng cách từ A đến mặt phẳng (BCD) bằng

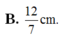

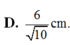
Cho tứ diện ABCD có cạnh DA vuông góc với mặt phẳng (ABC) và AB=3 cm, BC=4 cm, A D = 6 c m , AC=5 cm. Khoảng cách từ A đến mặt phẳng (BCD) bằng
A. 12 5 cm
B. 12 7 cm
C. 6 cm
D. 6 10 cm
Cho tứ diện ABCD có AB=BC=AC=BD=2a, AD= a 3 ; hai mặt phẳng (ACD) và (BCD) vuông góc với nhau. Diện tích mặt cầu ngoại tiếp tứ diện ABCD bằng
![]()
![]()
![]()
![]()
Cho tứ diện ABCD, có các cạnh DA, DB, DC đôi một vuông góc với nhau. Biết rằng DA = a, DB = a 2 , DC = 2a. Tính diện tích S của tam giác ABC.

A. S ABC = 14 9 a 2
B. S ABC = 14 6 a 2
C. S ABC = 14 4 a 2
D. S ABC = 14 2 a 2
Đáp án D
Kẻ DI ⊥ AB, DH ⊥ CI. Khi đó DH ⊥ (BCA).
Suy ra
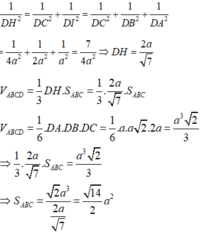
Cho hình tứ diện ABCD có DA = BC = 5, AB = 3, AC = 4. Biết DA vuông góc với mặt phẳng (ABC). Thể tích của khối tứ diện ABCD là:
a
B. V = 20
C. V = 30
D. V = 60
Đáp án A
Dễ thấy ∆ABC vuông tại A => SABC = 6
=> VS.ABC = 1 3 .6.5 = 10