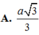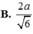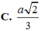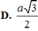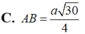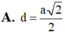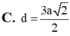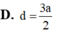Question

1. Cho tứ diện ABCD có AD vuông góc (ABC), AD=a√3. Góc giữa (ABC) và (DBC) bằng 60⁰. Gọi M là trung điểm AD. Tính khoảng cách từ M đến (BCD). 2. Cho hình chóp S.ABCD có SA vuông góc (ABCD), đáy ABCD là hình chữ nhật tâm O. Biết AD=2a, SA=a. Khoảng cách từ O đến (SCD) bằng

Answer 1

Câu 2: ABCD là hình chữ nhật có tâm O

=>O là trung điểm của AC

=>d(A;(SCD))=2d(O;(SCD))

Kẻ AH⊥SD tại H

ta có: CD⊥ AD(ABCD là hình chữ nhật)
CD⊥ SA(SA⊥(ABCD))

AD,SA cùng thuộc mp(SAD)

Do đó CD⊥(SAD)

=>CD⊥AH

Ta có: AH⊥SD

AH⊥CD
mà SD,CD cùng thuộc mp(SDC)

nên AH⊥(SCD)

=>AH là khoảng cách từ A đến mp(SCD)

Xét ΔSAD vuông tại A có AH là đường cao

nên \(\frac{1}{AH^2}=\frac{1}{AS^2}+\frac{1}{AD^2}=\frac{1}{\left(2a\right)^2}+\frac{1}{a^2}=\frac{1}{4a^2}+\frac{1}{a^2}=\frac{5}{4a^2}\)

=>\(AH^2=\frac{4a^2}{5}\)

=>\(AH=\frac{2a\sqrt5}{5}\)

=>\(d\left(A;\left(SCD\right)\right)=\frac{2a\sqrt5}{5}\)

=>\(d\left(O;\left(SCD\right)\right)=\frac{2a\sqrt5}{5}:2=\frac{a\sqrt5}{5}\)