Đặt a log2 3; b log5 6. Tính T log15 6 theo a, b.
Đọc tiếp
Đặt a = log2 3; b = log5 6. Tính T = log15 6 theo a, b.
Những câu hỏi liên quan
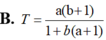
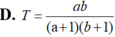
Đặt a= log23 . Hãy tính log2 48 theo a
A. 3+ 2a
B. 4+ 2a
C. 4+ a
D. 5- a
Chọn C
Ta có: log248= log2( 24. 3) = log224+ log23 = 4+ log23= 4+ a
Đúng 0
Bình luận (0)
Đặt log2 a, log3 b . Khi đó
log
5
12
bằng A.
2
a
+
b
1
-
a
B.
a
+
2
b
1
-
a
C.
2
a...
Đọc tiếp
Đặt log2 = a, log3 = b . Khi đó log 5 12 bằng
A. 2 a + b 1 - a
B. a + 2 b 1 - a
C. 2 a + b 1 + a
D. a + b 1 + a
Đặt
m
log
2
và
n
log
7.
Hãy biểu diễn
log
6125
7
theo m và n. A.
6
+
6
m
+
5
n
2
.
B.
1
2
6
−
6...
Đọc tiếp
Đặt m = log 2 và n = log 7. Hãy biểu diễn log 6125 7 theo m và n.
A. 6 + 6 m + 5 n 2 .
B. 1 2 6 − 6 n + 5 m .
C. 5 m + 6 n − 6.
D. 6 + 5 n − 6 m 2 .
Đáp án D.
Ta có:
log 6125 7 = log 6125 + log 7 = log 7 2 .125 + 1 2 log 7 = 2 log 7 + log 125 + 1 2 log 7 = 5 2 log 7 + log 5 3 = 5 2 n + 3 log 5 = 5 2 n + 3 1 − log 2 = 5 2 n + 3 − 3 m .
Đúng 0
Bình luận (0)
Đặt
α
log
2
,
β
log
3
,
γ
log
7
. Hãy biểu diễn
log
2016
theo
α
,
β
v
à
γ
A.
log
2016
2
α
-
5
β
-
γ
B.
log
2016...
Đọc tiếp
Đặt α = log 2 , β = log 3 , γ = log 7 . Hãy biểu diễn log 2016 theo α , β v à γ
A. log 2016 = 2 α - 5 β - γ
B. log 2016 = 5 α - 2 β - γ
C. log 2016 = 5 α + 2 β + γ
D. log 2016 = 10 α β γ
Cho bất phương trình
log
4
x
.
l
o
g
2
(
4
x
)
+
log
2
(
x
3
/
2
)
0
. Nếu đặt
t
l
o
g
2
x
, ta được bất phương trình nào sau đây A. ...
Đọc tiếp
Cho bất phương trình log 4 x . l o g 2 ( 4 x ) + log 2 ( x 3 / 2 ) > 0 . Nếu đặt t = l o g 2 x , ta được bất phương trình nào sau đây
A. t 2 + 14 t - 4 > 0
B. t 2 + 11 t - 3 > 0
C. t 2 + 14 t - 2 > 0
D. t 2 + 11 t - 2 > 0
Phương trình log 2 ( x + 3 ) + log 2 ( x - 1 ) = log 2 5 có nghiệm là:
A. x = 1
B. x = 2
C. x = 3
D. x = 0
Tìm tập nghiệm S của phương trình
l
o
g
2
(
x
-
1
)
+
l
o
g
2
(
x
+
1
)
3
A
.
S
-
3
;
3
B
.
S...
Đọc tiếp
Tìm tập nghiệm S của phương trình l o g 2 ( x - 1 ) + l o g 2 ( x + 1 ) = 3
A . S = - 3 ; 3
B . S = 10
C . S = 3
D . S = - 10 ; 10
Bất phương trình
log
2
(
3
x
−
2
)
log
2
(
6
−
5
x
)
có tập nghiệm là (a;b). Tổng a + b bằng A.
8
3
.
B.
28
15
.
C.
26
5
....
Đọc tiếp
Bất phương trình log 2 ( 3 x − 2 ) > log 2 ( 6 − 5 x ) có tập nghiệm là (a;b). Tổng a + b bằng
A. 8 3 .
B. 28 15 .
C. 26 5 .
D. 11 5 .
4 tháng 10 2021 lúc 22:33
Tính tổng tất cả các nghiệm của phương trình: \(\dfrac{1}{2}\).log2(x+3) = log2(x+1) + x2 - x - 4 + 2\(\sqrt{x+3}\)
ĐKXĐ: \(x>-1\)
Bước quan trọng nhất là tách hàm
\(\Leftrightarrow log_2\sqrt{x+3}-2\sqrt{x+3}+\left(x+3\right)=log_2\left(x+1\right)-2\left(x+1\right)+\left(x+1\right)^2\)
Đến đây coi như xong \(\Rightarrow\sqrt{x+3}=x+1\Rightarrow x=1\)
Đúng 1
Bình luận (0)