Ta có: 2yz + y² + z² - x²

= (y² + 2yz + z²) - x²

= (y + z)² - x²

= (y + z + x)(y + z - x)

= 2a(y + z + x - 2x)

= 2a(2a - 2x)

= 2a.2(a - x)

= 4a(a - x) --> Đpcm

giai di 

k roi giai

Hình như thiếu thiếu gì đó

ko thiếu đâu bạn

x+y=a+b nữa thì phải.Mình đọc bài này trong sách rồi

a) Ta có \(\left(a-b\right)^2\ge0\)

\(\Leftrightarrow a^2-2ab+b^2\ge0\)

\(\Leftrightarrow a^2+b^2\ge2ab\)

\(\Leftrightarrow\frac{a^2+b^2}{2}\ge ab\)( chia 2 vế cho 2 )

b) \(\frac{a+1}{a}\)chưa lớn hơn hoặc bằng 2 đc , bạn thay a=2 vào thì 3/2<2

c) Ta có \(x^2\ge0\);\(y^2\ge0\);\(z^2\ge0\)

nên \(x^2+y^2+z^2\ge0\)

\(\Rightarrow x^2+y^2+z^2+3\ge3\)

Ta có \(\left(a-b\right)^2\ge0\)

\(\Leftrightarrow a^2-2ab+b^2\ge0\)

\(\Leftrightarrow a^2-2ab+b^2\ge0\)

\(\Leftrightarrow a^2+b^2\ge2ab\Leftrightarrow\frac{a^2+b^2}{2}\ge ab\)

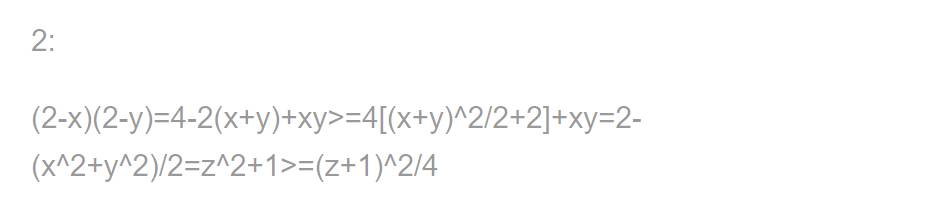
Tương tự, ta được:

\(\left(2-y\right)\left(2-z\right)>=\dfrac{\left(x+1\right)^2}{4}\)

và \(\left(2-z\right)\left(2-x\right)>=\left(\dfrac{y+1}{2}\right)^2\)

=>8(2-x)(2-y)(2-z)>=(x+1)(y+1)(z+1)

(x+yz)(y+zx)<=(x+y+yz+xz)^2/4=(x+y)^2*(z+1)^2/4<=(x^2+y^2)(z+1)^2/4

Tương tự, ta cũng co:

\(\left(y+xz\right)\left(z+y\right)< =\dfrac{\left(y^2+z^2\right)\left(x+1\right)^2}{2}\)

và \(\left(z+xy\right)\left(x+yz\right)< =\dfrac{\left(z^2+x^2\right)\left(y+1\right)^2}{2}\)

Do đó, ta được:

\(\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)< =\left(x+1\right)\left(y+1\right)\left(z+1\right)\)

=>ĐPCM

    \(\left(a^2+b^2\right)\left(x^2+y^2\right)=\left(ax+by\right)^2\)

\(\Rightarrow a^2x^2+a^2y^2+b^2x^2+b^2y^2=a^2x^2+2axby+b^2y^2\)

\(\Rightarrow a^2y^2+b^2x^2=2axby\)

\(\Rightarrow a^2y^2-2axby+b^2x^2=0\)

\(\Rightarrow\left(ay\right)^2-2.ay.bx+\left(bx\right)^2=0\)

\(\Rightarrow\left(ay-bx\right)^2=0\)

\(\Rightarrow ay-bx=0\Rightarrow ay=bx\Rightarrow\frac{a}{x}=\frac{b}{y}\)