Cách 1:Xét tứ giác ADBC có 

AB và CD cắt nhau tại O là trung điểm của mỗi đường

=>ADBC là hình bình hành 

=>AC//BD(đl)

Cách 2 Chứng minh được \(\Delta AOC=\Delta BOD\left(AO=OC;\widehat{AOC}=\widehat{BOD};OC=OD\right)\)

\(\Rightarrow\widehat{CAO}=\widehat{DBO}\)Hay \(\widehat{CAB}=\widehat{DBA}\)

Hai góc này ở vị trí so le trong bằng nhau

=> AC//BD

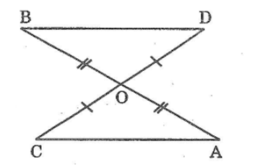
Xét Δ AOC và Δ BOD, ta có:

OA = OB ( Vì O là trung điểm của AB )

∠(AOC) =∠(BOD) (đối đỉnh)

OC = OD ( Vì O là trung điểm của CD)

Suy ra: ΔAOC = ΔBOD (c.g.c)

⇒∠A =∠B (hai góc tương ứng)

Vậy: AC // BD (vì có hai góc so le trong bằng nhau)

Ta có hình vẽ:

Xét Δ AOC và Δ BOD có:

OA = OB (gt)

AOC = BOD (đối đỉnh)

OC = OD (gt)

Do đó, Δ AOC = Δ BOD (c.g.c)

=> ACO = ODB (2 góc tương ứng)

Mà ACO và ODB là 2 góc so le trong nên AC // BD (đpcm)

Ta có hình vẽ sau:

Xét ΔOAC và ΔOBD có:

OA = OB (gt)

\(\widehat{O_1}\) = \(\widehat{O_2}\) (2 góc đối đỉnh)

OC = OD (gt)

\(\Rightarrow\) ΔOAC = ΔOBD (c.g.c)

\(\Rightarrow\) \(\widehat{C}\) = \(\widehat{D}\) (2 góc tương ứng)

Mà 2 góc này lại ở vị trí so le trong nên

\(\Rightarrow\) AC // BD(đpcm)

 mik ko bt lm

a: Xét tứ giác ACBD có 

O là trung điểm của đường chéo AB

O là trung điểm của đường chéo CD

Do đó: ACBD là hình bình hành

Suy ra: AC//DB và AC=DB

b: Ta có: ACBD là hình bình hành

nên AD//CB và AD=CB

Xét \(\Delta AOD\) và \(\Delta BOC\), ta có: AO = BO (vì O là trung điểm của AB); \(\widehat{AOD}=\widehat{BOC}\) (đối đỉnh); OD = OC (vì O là trung điểm của CD)

\(\Rightarrow\Delta AOD=\Delta BOC\left(c-g-c\right)\)

\(\Rightarrow\widehat{DAO}=\widehat{OBC}\) (2 góc tương ứng)

Mà hai góc này ở vị trí so le cho nên AC // BD.

a: Xét tứ giác ACBD có 

O là trung điểm của AB

O là trung điểm của CD

Do đó: ACBD là hình bình hành

Suy ra: AD//BC; AC//BD

Xét tam giác AOD và BOC có:  AO = BO (vì O là trung điểm của AB)  ; góc AOD = BOC (đối đỉnh) ; OD = OC (vì O là trung điểm của CD)

=> tam giác AOD = BOC  (c - g - c)

=> góc DAO = OBC ( 2 góc tương ứng)

Mà hai góc này ở vị trí so le trong nên AC // BD