Các đườg cao AN và BM của tam giác ABC có 3 góc nhọn cắt nhau tại H và cắt đườg tròn (O; R ) ngoại tiếp tam giác ABC lần lượt tại D và E .
a) chứg minh CD = CE
b) chứg minh H và D đối xứng nhau qua BC
Những câu hỏi liên quan
Cho tam giác abc có ba góc nhọn nội tiếp đường tròn (O). Hai đường cao AM và CN của tam giác ABC cắt nhau tại H. Gọi D và E là giao điểm thứ hai của tia AM và tia CN vs đườg tròn(O).chứng minh: a. Tứ giác BNHM nội tiếp b.BD=BE=BH c.ED//MN
a) Xét tứ giác BNHM có
\(\widehat{BNH}\) và \(\widehat{BMH}\) là hai góc đối
\(\widehat{BNH}+\widehat{BMH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: BNHM là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 0
Bình luận (1)
Cho tam giác ABC có 3 góc nhọn. các điểm M,N thứ tự là trug điểm của BC và AC. các đườg trug trực của BC và AC cắt nhau tại O. Qua A kẻ đườg thẳg sog2 vs OM. qua B kẻ đg thẳg sog2 vs ON chúg cắt nhau tại H. a) Nối MN. tam giác AHB ~ tam giác nào? b) gọi G là trọg tâm của tam giác ABC. CMR: M,O,G thẳg hàg
có ai kết bạn với mk ko ? mk mới học lớp 5 à !!!
Đúng 0
Bình luận (0)
Tam giác ABC nội tiếp đườg tròn tâm O
AB<AC, đườg cao BD cắt đườg cao CE tại H
M là trung điểm BC , MH cắt đườg tròn tại N
CMR: A,D,H,E,N cùg thuộc 1 đườg tròn
Tìm lun đườg tròn đó
Các đường cao AN và BM của tam giác ABC có ba góc nhọn cắt nhau tại H và cắt đường tròn (O;R) ngoại tiếp tam giác ABC lần lượt tại D và E
Biết MN/AB =1/2 Tính MN theo R
Cho tam giác ABC có ba góc nhọn nội tiếp (O;R). Hai đường cao AN và BM của tam giác ABC cắt nhau tại I a) Chứng minh tứ giác IMCN nội tiêpa một đường tròn b) Chứng minh: IA.IN=IB.IM c) Tia BM cắt (O) tại H. Chứng minh AI = AH
a: góc INC+góc IMC=90+90=180 độ
=>IMCN nội tiếp
b: Xét ΔIMA vuông tại M và ΔINB vuông tại N có
góc MIA=góc NIB
=>ΔIMA đồng dạng với ΔINB
=>IM/IN=IA/IB
=>IM*IB=IN*IA
c: góc AHI=góc ACB
=>góc AHI=góc AIH
=>AH=AI
Đúng 0
Bình luận (0)
Cho tam giác ABC có ba góc nhọn nội tiếp (O;R). Hai đường cao AN và BM của tam giác ABC cắt nhau tại I a) Chứng minh tứ giác IMCN nội tiêpa một đường tròn b) Chứng minh: IA.IN=IB.IM c) Tia BM cắt (O) tại H. Chứng minh AI = AH
a: góc INC+góc IMC=90+90=180 độ
=>IMCN nội tiếp
b: Xét ΔIMA vuông tại M và ΔINB vuông tại N có
góc MIA=góc NIB
=>ΔIMA đồng dạng với ΔINB
=>IM/IN=IA/IB
=>IM*IB=IN*IA
c: góc AHI=góc ACB
=>góc AHI=góc AIH
=>AH=AI
Đúng 0
Bình luận (0)
Cho tam giác abc luôn có 3 góc nhọn, các đườg cao AD,BE,CF cắt nhau tại H, gọi K là gđ của AH
a, AD.HK=AK.HD
b,tìm Max AD.HD
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O). Hai đường cao AD và CE cắt nhau tại H. Tia BO cắt (O) tại điểm thứ hai M. I là giao điểm của BM và DE
b) Chứng minh BA.BE = BD.BD
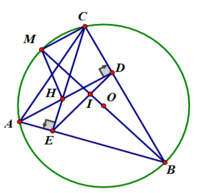
b) Xét ΔABD và Δ CEB có:
∠(ABC) chung
∠(ADB) = ∠(CEB) = 90 0
⇒ ΔABD ∼ Δ CBE (g.g)
Đúng 0
Bình luận (0)
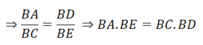
Cho tam giác ABC có ba góc nhọn nội tiếp (O,R). Hai đường cao AN và BM của tam giác ABC cắt nhau tại I
a Chứng minh tứ giác IMCN nội tiếp được một đường tròn
b chứng minh IA.IN=IM.IB
c tia BM cắt (O) tại H Chứng minh AI=AH
a: góc INC+góc IMC=180 độ
=>INCM nội tiếp
b: Xét ΔINB vuông tại N và ΔIMA vuông tại M có
góc NIB=góc MIA
=>ΔINB đồng dạng với ΔIMA
=>IN/IM=IB/IA
=>IN*IA=IM*IB
c: góc AIH=góc BIN=góc BCA
=>góc AIH=góc AHI
=>AI=AH
Đúng 0
Bình luận (0)