GT: ΔMNP cân tại M; MH ⊥ NP tại H; MK=MP; EL ⊥ HP tại L; Trung tuyến HE: ME = EP = MP/2
KL: a) Chứng minh △MNH=△MPH
b) Chứng minh ΔMNK cân
c) Chứng minh PL là đường phân giác góc PEH
d) EH // MN
Những câu hỏi liên quan
24 tháng 4 2023 lúc 21:20
Cho ΔMNP cân tại M ( M<\(90^o\)). kẻ NH⊥MP ( H ϵ MP ), PK ⊥ MN ( Kϵ MN ).NH và PK cắt nhau tại E.
a) chứng minh ΔNMP = ΔPKN
Xet ΔKNP vuông tại K và ΔHPN vuông tại H có
PN chung
góc KNP=góc HPN
=>ΔKNP=ΔHPN
Đúng 0
Bình luận (0)
cho ΔMNP cân tại M, vẽ MH⊥NP
a)CM: ΔMHN=ΔMHP
b)CM: MH là phân giác của ΔMNP
c) Gọi K là điểm nằm trên tia đối của tia HM. CM: ΔKNP cân
a: Xét ΔMHN vuông tại H và ΔMHP vuông tại H có
MN=MP
MH chung
=>ΔMHN=ΔMHP
b: ΔMNP cân tại M
mà MH là đường cao
nên MH là phân giác
Đúng 0
Bình luận (0)
Cho ΔMNP cân tại M ( M < 90°). Kẻ NH ⊥ MP(H∈ MP), PK ⊥ MN (K∈ MN).NH và PK cắt nhau tại E. a) Chứng minh Δ NHP=ΔPKN b) Chứng minh ΔENP cân c) Chứng minh ME là đường phân giác của góc NMP
a: Xét ΔKNP vuông tại K và ΔHPN vuông tại H có
PN chung
góc KNP=góc HPN
=>ΔKNP=ΔHPN
b: Xét ΔENP có góc ENP=góc EPN
nên ΔENP cân tại E
c: Xét ΔMNE và ΔMPE có
MN=MP
EN=EP
ME chung
=>ΔMNE=ΔMPE
=>góc NME=góc KME
=>ME là phân giác của góc NMP
Đúng 0
Bình luận (0)
24 tháng 10 2021 lúc 18:55
Câu 3:
ΔMNP cân tại P. Biết góc N có số đo bằng 500. Số đo góc P bằng:
· A. 800
· B. 100
· C. 500
· D. 1300
Tính thể tích khối chóp S.MNP biết
S
M
a
3
, ΔMNP đều, ΔSMN vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. A.
2
a
3
3
B.
3
2
a
3
4
C....
Đọc tiếp
Tính thể tích khối chóp S.MNP biết S M = a 3 , ΔMNP đều, ΔSMN vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy.
A. 2 a 3 3
B. 3 2 a 3 4
C. 2 a 3 6
D. 3 2 a 3 2
Đáp án B
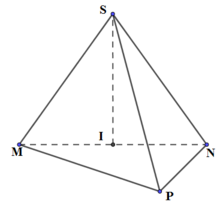
ΔSMN vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy, gọi I là trung điểm của MN ⇒ SI⊥(ABC) và 
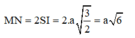
ΔMNP đều
Thể tích khối chóp S.MNP là
Đúng 0
Bình luận (0)
1 tháng 5 2023 lúc 20:56
d7câu 7: Cho ΔMNP cân tại M; các đường trung trực MN và MP cắt nhau tại O khi đó :A.ONOQ B.OMNOMPC.MONMOP D.điểm o cách đều 3 đỉnh của ΔMNPCâu 8: các đường cao của tam giác ABC cắt nhau tại H thì A. điểm H là tọng tâm của tam giác ABC B. điểm H cách đều 3 cạnh của tam giác C. điểm H cách đều 3 đỉnh A;B;CD. điểm H là trực tâm của tam giác ABCCâu 10: Cho ABC nhọn có góc B lớn hơn góc C gọi H là chân đường vuông góc kẻ từ A tới BC khi đó A.ABAHACB.ABACC.AHABACD.AHACAB
Đọc tiếp
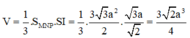
d7
câu 7: Cho ΔMNP cân tại M; các đường trung trực MN và MP cắt nhau tại O khi đó :
A.ON>OQ B.OMN>OMP
C.MON>MOP D.điểm o cách đều 3 đỉnh của ΔMNP
Câu 8: các đường cao của tam giác ABC cắt nhau tại H thì
A. điểm H là tọng tâm của tam giác ABC B. điểm H cách đều 3 cạnh của tam giác
C. điểm H cách đều 3 đỉnh A;B;C
D. điểm H là trực tâm của tam giác ABC
Câu 10: Cho ABC nhọn có góc B lớn hơn góc C gọi H là chân đường vuông góc kẻ từ A tới BC khi đó
A.AB<AH<AC
B.AB>AC
C.AH<AB<AC
D.AH<AC<AB
`7,`
`@` Theo tính chất điểm đồng quy của `3` đường trung trực (cách đều các đỉnh của tam giác)
`-> D`
`8,`
`-` Giao điểm của `3` đường cao là trực tâm
`-> D.`
`10,`
`@` Theo định lý giữa đường vuông góc và đường xiên (Trong các đường xiên và đường vuông góc kẻ từ 1 điểm đến 1 đường thẳng thì đường vuông góc là đường ngắn nhất)
`-> C`
Đúng 4
Bình luận (1)
Cho ΔMNP vuông tại M có MN = 9cm, MP = 12cm. Vẽ MH vuông góc với NP tại H
a) Chứng minh ΔHNM và ΔMNP đồng dạng
b) Tính diện tích tam giác MHP
c) Vẽ tia phân giác MD của góc NMH (D ∈ NH). Chứng minh: ND.MP = DH.NP
a: Xét ΔHNM vuông tại H và ΔMNP vuông tại M có
góc N chung
=>ΔHMN đồng dạng vói ΔMNP
b: \(NP=\sqrt{9^2+12^2}=15\left(cm\right)\)
MH=9*12/15=108/15=7,2cm
HP=12^2/15=9,6cm
S MHP=1/2*9,6*7,2=34,56cm2
Đúng 1
Bình luận (0)
Cho ΔMNP cân tại M có MN=MP=5cm, NP=6cm. Kẻ MI vuông góc với MP(I∈MP)
a) chứng minh ΔMIN=ΔMIP
b) từ I kẻ IE vuông góc với MN(E∈MN) và IF vuông góc với MP(F∈MP). Chứng minh ME=MF. Tính độ dài của đoạn thẳng MI
a: Xét ΔMIN vuông tại I và ΔMIP vuông tại I có
MN=MP
MI chung
=>ΔMIN=ΔMIP
b: Xét ΔMEI vuông tại E và ΔMFI vuông tại F có
MI chung
góc EMI=góc FMI
=>ΔMEI=ΔMFI
=>ME=MF
IN=IP=6/2=3cm
=>MI=4cm
Đúng 0
Bình luận (0)
Bài1:Cho ΔMNP vuông tại N. Tính độ dài MN biết MP√30cm,NP√14 cmBài2:Cho ΔABC cân tại A. Biết AB2cm. Tính BCBài3:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH6cm,HB4cm,HC9cmBài4:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH4cm,HB2cm,HC8cmBài5:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB4cm,HB2cm,HC8cm.Tính BC,AH,ACBài6:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB6cm,AC8cm và dfrac{HB}{HC}dfrac{9}{16}Tính HB,HC
Đọc tiếp
Bài1:Cho ΔMNP vuông tại N. Tính độ dài MN biết MP=√30cm,NP=√14 cm
Bài2:Cho ΔABC cân tại A. Biết AB=2cm. Tính BC
Bài3:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH=6cm,HB=4cm,HC=9cm
Bài4:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH=4cm,HB=2cm,HC=8cm
Bài5:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB=4cm,HB=2cm,HC=8cm.Tính BC,AH,AC
Bài6:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB=6cm,AC=8cm và \(\dfrac{HB}{HC}\)=\(\dfrac{9}{16}\)Tính HB,HC
Bài 3:
\(AB=\sqrt{AH^2+BH^2}=\sqrt{6^2+4^2}=2\sqrt{13}\left(cm\right)\)
BC=13cm
=>\(AC=3\sqrt{13}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho ΔMNP,MH⊥NP tại H,MN=3cm MP=4cm NH=1,8cm
a,vẽ hình
b,tính MH,HP
c,Chứng minh ΔMNP là tam giác vuông
b: \(MH=\sqrt{3^2-1.8^2}=2.4\left(cm\right)\)
\(PH=\sqrt{4^2-2.4^2}=3.2\left(cm\right)\)
c: Xét ΔMNP có \(NP^2=MN^2+MP^2\)
nên ΔMNP vuông tại M
Đúng 0
Bình luận (0)