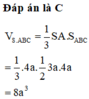Cho tam giác ABC có AB=AC=4a; BC=2a. Tính bán kính đường tròn ngoại tiếp tam giác ABC.

Những câu hỏi liên quan
Cho tam giác ABC có AB 2a; AC 4a và góc BAC
120
0
. Tính diện tích tam giác ABC ? A.
S
8
a
2
. B.
S
2
a
2
3
C.
S
a
2
3
. D. ...
Đọc tiếp
Cho tam giác ABC có AB = 2a; AC = 4a và góc BAC = 120 0 . Tính diện tích tam giác ABC ?
A. S = 8 a 2 .
B. S = 2 a 2 3
C. S = a 2 3 .
D. S = 3 a 2 3
Cho tam giác ABC có AB=AC=4a;BC=2a .Bán kính đường tròn ngoại tiếp tam giác ABC bằng
Cho tam giác ABC có AB=AC=4a; BC=2a. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Gọi (O;R) là đt ngoại tiếp tam giác ABC
Gọi D là gđ của AO và đt (O)
Kẻ đường cao AH => AH vừa là đường cao, đồng thời là đường trung tuyến
ÁP dụng định lí pytago vào tam giác AHB vuông tại H có:\(AH=\sqrt{AB^2-BH^2}=\sqrt{\left(4a\right)^2-\dfrac{BC^2}{4}}\)\(=\sqrt{16a^2-a^2}=a\sqrt{15}\)
Chứng minh được: \(\Delta AHB\sim ACD\left(g.g\right)\)
\(\Rightarrow\dfrac{AH}{AC}=\dfrac{AB}{AD}\) \(\Leftrightarrow AD=\dfrac{AB.AC}{AH}=\dfrac{4a.4a}{a\sqrt{15}}=\dfrac{16a\sqrt{15}}{15}\)
\(\Rightarrow R=\dfrac{AD}{2}=\dfrac{8a\sqrt{15}}{15}\)
Đúng 2
Bình luận (0)
cho tam giác ABC vuông tại A . Có AB 3a,AC 4a. Dựng và tính độ dài véctơ AB véctơ AC
Cho hình chóp S.ABC có SA vuông góc với (ABC) tam giác ABC vuông tại A, AB=3a,AC=4a,SA=4a. Thể tích khối chóp S.ABC là:
A. 2 a 3
B. 6 a 3
C. 8 a 3
D. 9 a 3
cho tam giác ABC vuông tại A . Có AB = 3a,AC =4a. Dựng và tính độ dài véctơ AB +véctơ AC
Cho tam giác ABC có BC=4a.; CA=4a;AB=3a. Đường trung trực của đoạn AC cắt đường phân giác trong của góc BAC tại K. CM trung điểm của đoạn AK là tâm đường tròn nội tiếp tam giác ABC.
Cho tam giác ABC vuông tại A có AB = 3a, AC = 4a. Khi đó độ dài vecto BC là
Lời giải:
$|\overrightarrow{BC}|=BC=\sqrt{AB^2+AC^2}=\sqrt{(3a)^2+(4a)^2}=5a$ theo định lý Pitago.
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A có AB=3a; AC=4a. Khi đó độ dài của vectơ BC là bn?




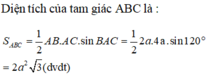



 Chúc bạn học tốt
Chúc bạn học tốt