a: f(x) chiahết cho g(x)

=>\(x^4-x^2-3x^3+3x+\left(b+1\right)x^2-\left(b+1\right)+\left(a-3\right)x+2b+1⋮x^2-1\)

=>a-3=0 và 2b+1=0

=>a=3 và b=-1/2

b: A=2x^2-3x

=2(x^2-3/2x)

=2(x^2-2*x*3/4+9/16-9/16)

=2(x-3/4)^2-9/8>=-9/8

Dấu = xảy ra khi x=3/4

bạn trúc giang sai rồi -4 nhân -3x sao lại bằng -12x

\(f\left(x\right)⋮g\left(x\right)\)

\(\Leftrightarrow x^4-3x^3+4x^2-x^2+3x-4+\left(a-3\right)x+\left(b+4\right)⋮x^2-3x+4\)

\(\Leftrightarrow\left(a,b\right)=\left(3;-4\right)\)

Ta có 

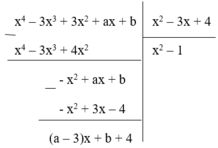
Phần dư của phép chia f(x) cho g(x) là R = (a – 3)x + b + 4. Để phép chia trên là phép chia hết thì R = 0, Ɐx

ó (a – 3)x + b + 4 = 0, Ɐx ó   a - 3 = 0 b + 4 = 0

ó a = 3 b = - 4 => ab = -12

Đáp án cần chọn là: A

a) x²y+xy+x+1= (x²y+xy)+(x+1)=xy(x+10+(x+1)=(x+1)(xy+1)

b) x²-(a+b)x+ab=x²-ax-bx+ab=(x²-ax)-(bx-ab)=x(x-a)-b(x-a)=(x-a)(x-b)

c) ax²+ay-bx²-by=(ax²+ay)-(bx²+by)=a(x²+y)-b(x²+y)=(a-b)(x²+y)

d) ax-2x-a²+2a=(ax-2x)-(a²-2a)=x(a-2)-a(a-2)=(a-2)(x-a)

e) 2x²+4ax+x+2a=(2x²+4ax)+(x+2a)=2x(x+2a)+(x+2a)=(x+2a)(2x+1)

f) x³+ax²+x+a=(x³+ax²)+(x+a)=x²(x+a)+(x+a)=(x²+1)(x+a)

g: Ta có: \(x^4+2x^3-4x-4\)

\(=\left(x^2-2\right)\left(x^2+2\right)-2x\left(x^2-2\right)\)

\(=\left(x^2-2\right)\cdot\left(x^2+2x+2\right)\)

Đặt \(g\left(x\right)=f\left(x\right)-10\) (bậc 4)

\(\Leftrightarrow\left\{{}\begin{matrix}g\left(1\right)=0\\g\left(2\right)=0\\g\left(3\right)=0\end{matrix}\right.\Leftrightarrow g\left(x\right)=\left(x-1\right)\left(x-2\right)\left(x-3\right)\left(x-m\right)\) (m là hằng số)

\(\Leftrightarrow f\left(x\right)=\left(x-1\right)\left(x-2\right)\left(x-3\right)\left(x-m\right)-10\\ \Leftrightarrow f\left(9\right)=8\cdot7\cdot6\left(9-m\right)-10=336\left(9-m\right)-10\\ f\left(-5\right)=\left(-6\right)\left(-7\right)\left(-8\right)\left(-5-m\right)-10=336\left(m+5\right)-10\)

Vậy \(A=336\left(9-m\right)+336\left(m+5\right)-20=4684\)

Chúc bạn hok tốt <3

khó thế ai làm được? ?????????

:v thế mới đi hỏi 

dễ nhưng lm mất tg lắm