cho tam giác ABC .Trên tia đối của tia AB và AC lấy E và F sao cho AE=AB; AF=AC
a, C/M EF=BC
b, Vẽ AH vuông góc với BC cắt AF tại M
C/M AM vuông góc với EF
Những câu hỏi liên quan
Cho tam giác ABC. Trên cạnh BC lấy điểm M. Trên tia đối của tia AB lấy D sao cho AB=AD. Trên tia đối của tia AC lấy E sao cho AC=AE. Trên tia đối của tia AM lấy F sao cho AM=AF. Chứng minh D, E, F thẳng hàng.
Cho tam giác ABC có AB < AC. vẽ tia đối của tia AB, trên đó lấy điểm D sao cho AD = AC. Vẽ tia đối của AC, trên đó lấy điểm E sao cho AE = AB. So sánh tam giác ABC và tam giác AED.
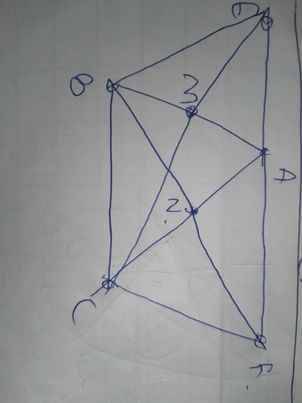
cho tam giác abc có góc b+c =60độ trên đường phân giác AD của góc A lấy điểm I trên tia đối của tia AC lấy E sao cho AE=AI trên tia đối của tia AB lấy F sao cho AE= AI=AF cm AB và AC là đường trung trực của IE vaIF . cm tam giác IEF đều .cm IA vuông góc với EF
a: góc A=180-60=120 dộ
=>góc EAB=60 độ=góc BAI
Xet ΔEAB và ΔIAB có
góc EAB=góc IAB
AB chung
EA=IA
=>ΔEAB=ΔIAB
=>BE=BI
=>AB là trung trực của IE
Chứng minh tương tự, ta được: AC là trung trực của IF
b: góc EAB=góc FAC=60 độ
=>góc EAB+góc BAI=góc FAC+góc IAC
=>góc EAI=góc FAI
Xét ΔEAI và ΔFAI có
AI chung
góc EAI=góc FAI
AE=AF
=>ΔEAI=ΔFAI
=>EI=FI
=>ΔIFE cân tại I
=>góc EIF=2*góc AIE
ΔEAI cân tại A
=>góc AIE=(180-60-60)/2=30 độ
=>góc EIF=60 độ
=>ΔIEF đều
c: góc AIE=góc AIF
=>AI là phân giác của góc EIF
mà ΔEIF đều
nên AI vuông góc EF
Đúng 0
Bình luận (0)
cho tam giác ABC . Trên tia đối của tia AB lấy AD = AC , Trên tia đối của tia AC lấy điểm E sao cho AE = AB a) so sánh tam giác ABC và tam giác ADE b) Gọi M và N lần lượt là trung điểm của AC và ED . CMR CM = DN
1. Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của AB và AC. Trên tia đối của tia MC lấy E sao cho: ME = MC. Trên tia đối của tia NB lấy F sao cho: NF = NB. Chứng minh:
a. Tam giác AME= Tam giác BMC
b. Tam giác AFN = tam giác CBN.
c. AE// BC
d. A là trung điểm của EF
a: Xét ΔAME và ΔBMC có
MA=MB
\(\widehat{AME}=\widehat{BMC}\)(hai góc đối đỉnh)
ME=MC
Do đó: ΔAME=ΔBMC
b: Xét ΔAFN và ΔCBN có
NA=NC
\(\widehat{ANF}=\widehat{CNB}\)(hai góc đối đỉnh)
NF=NB
Do đó: ΔAFN=ΔCBN
c: ΔAME=ΔBMC
=>\(\widehat{MAE}=\widehat{MBC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AE//BC
d: ΔAME=ΔBMC
=>AE=BC
ΔANF=ΔCNB
=>\(\widehat{NAF}=\widehat{NCB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AF//BC
ΔANF=ΔCNB
=>AF=CB
Ta có: AF=CB
AE=BC
Do đó: AE=AF
Ta có: AE//BC
AF//BC
AE,AF có điểm chung là A
Do đó: E,A,F thẳng hàng
mà AE=AF
nên A là trung điểm của EF
Đúng 1
Bình luận (0)
Cho tam giác ABC có AB < AC. Trên tia đối của tia BC lấy điểm D sao cho BD = AB. Trên tia đối của tia CB lấy điểm E sao cho CE = AC. So sánh:
a) A D C ^ và A E B ^ ;
b) AD và AE.
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD =AC và trên tia đối của AC lấy điểm E sao cho AE = AB. CM : BCDE là hình thang
hai tam giác EAD = BAC ( c - g -c)
=> góc DEA = CBA
tam giác EAB đông dạng CAD (c - g - c)
=> goc AEB = ACD
=> EB // CD
lại có BED = BEA + AED
góc EBC = EBA + ABC
mà góc BEA = EBA ( tam giác BAE cân taịA)
AED = ABC (cmt)
=> BCDE la hinh thang can
Đúng 0
Bình luận (0)
cho tam giác ABC có AB < AC, trên cạnh BC lấy điểm E sao cho AE = AB. Tia phân giác của góc A cắt BC tại D. chứng minh tam giác ABD = tam giác AED. Tia AB cắt ED tại K và chứn minh AK = AC. Trên tia đối của tia AB lấy điểm F sao cho FA = AB và chứng minh rằng FE song song với AD
a: Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
Do đo: ΔABD=ΔAED
Suy ra: DB=DE
b: Xét ΔDBH và ΔDEC có
góc DBH=góc DEC
DB=DE
góc BDH=góc EDC
Do đó: ΔDBH=ΔDEC
c: Ta có: ΔDBH=ΔDEC
nên góc DHB=góc DCE
d: Ta có: AH=AB+BH
AC=AE+EC
mà AB=AE; BH=EC
nên AH=AC
Đúng 0
Bình luận (0)
Cho tam giác ABC. Trên tia đối của AB lấy điểm D sao cho AD= AC và trên tia đối của tia AC lấy điểm E sao cho AE= AB. Chứng minh BCDE là hình thang
Hình:
Giải:
Ta có:
\(AB+AD=AC+AE\) (Vì \(AB=AE;AC=AD\))
\(\Leftrightarrow BD=CE\)
=> Tứ giác BCDE là hình thang (vì trong hình thang hai đường chéo bằng nhau)
Vậy tứ giác BCDE là hình thang (đpcm)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A (AB < AC).Trên tia đối của tia AC lấy điểm D sao cho AD = AB. Trên tia đối của tia AB lấy điểm E sao cho AE = AC. a) Chứng minh: BC = DE. b) Chứng minh: tam giác ABD vuông cân và BD // CE. c) Kẻ đường cao AH của tam giác ABC tia AH cắt cạnh DE tại M. từ A kẻ đường vuông góc CM tại K, đường thẳng này cắt BC tại N . Chứng minh: NM // AB. d) Chứng minh: AM = DE
a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
Do đó: ΔABC=ΔADE
=>BC=DE
b: Xét ΔABD vuông tại A có AB=AD
nên ΔABD vuông cân tại A
=>\(\widehat{ABD}=\widehat{ADB}=45^0\)
Xét ΔAEC vuông tại A có AE=AC
nên ΔAEC vuông cân tại A
=>\(\widehat{AEC}=\widehat{ACE}=45^0\)
Ta có: \(\widehat{ABD}=\widehat{AEC}\left(=45^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên BD//CE
Đúng 1
Bình luận (0)