Question

1. Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của AB và AC. Trên tia đối của tia MC lấy E sao cho: ME = MC. Trên tia đối của tia NB lấy F sao cho: NF = NB. Chứng minh:

a. Tam giác AME= Tam giác BMC

b. Tam giác AFN = tam giác CBN.

c. AE// BC

d. A là trung điểm của EF 

Answer 1

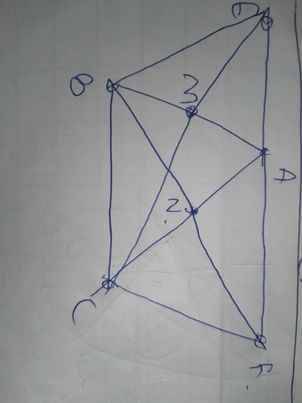
a: Xét ΔAME và ΔBMC có

MA=MB

\(\widehat{AME}=\widehat{BMC}\)(hai góc đối đỉnh)

ME=MC

Do đó: ΔAME=ΔBMC

b: Xét ΔAFN và ΔCBN có

NA=NC

\(\widehat{ANF}=\widehat{CNB}\)(hai góc đối đỉnh)

NF=NB

Do đó: ΔAFN=ΔCBN

c: ΔAME=ΔBMC

=>\(\widehat{MAE}=\widehat{MBC}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AE//BC

d: ΔAME=ΔBMC

=>AE=BC

ΔANF=ΔCNB

=>\(\widehat{NAF}=\widehat{NCB}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AF//BC

ΔANF=ΔCNB

=>AF=CB

Ta có: AF=CB

AE=BC

Do đó: AE=AF

Ta có: AE//BC

AF//BC

AE,AF có điểm chung là A

Do đó: E,A,F thẳng hàng

mà AE=AF

nên A là trung điểm của EF