Bài 1. Cho ABC (AB< AC) nội tiếp đường tròn (O). Lấy điểm D trên cạnh BC; AD cắt
cung BC ở E. Chứng minh rằng:
a) AEC > AEB (góc AEC > góc AEB) b) AB.CD = AD.CE

Những câu hỏi liên quan
Bài 1. Cho ABC (AB< AC) nội tiếp đường tròn (O). Lấy điểm D trên cạnh BC; AD cắt cung BC ở E. Chứng minh rằng: a) AEC > AEB (góc AEC > góc AEB) b) AB.CD = AD.CE
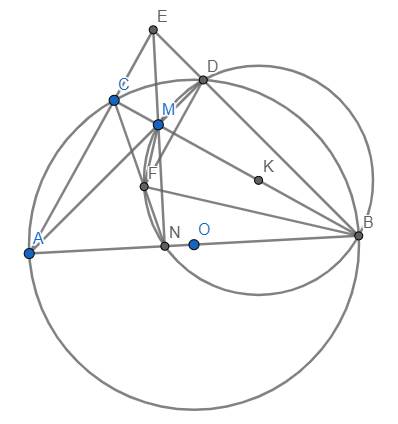
Cho tam giác ABC nội tiếp đường tròn (O), đường kính AB 2R Trên cạnh BC lấy điểm M ( M khác B khác C ) . Đường thẳng AM cắt đường tròn (O) tại điểm D, đường thẳng BD cắt AC tại E. Đường tròn tâm K ngoại tiếp tam giác MBD cắt đường kính AB tại điểm thứ hai N ( N khác B). Đường thẳng CN cắt đường tròn (K) tại F.
1) Chứng minh DF song song với AE.
2) Chứng minh rằng: BD.BE + AM.AD có giá trị không đổi.
Đọc tiếp
Cho tam giác ABC nội tiếp đường tròn (O), đường kính AB = 2R Trên cạnh BC lấy điểm M ( M khác B khác C ) . Đường thẳng AM cắt đường tròn (O) tại điểm D, đường thẳng BD cắt AC tại E. Đường tròn tâm K ngoại tiếp tam giác MBD cắt đường kính AB tại điểm thứ hai N ( N khác B). Đường thẳng CN cắt đường tròn (K) tại F.
1) Chứng minh DF song song với AE.
2) Chứng minh rằng: BD.BE + AM.AD có giá trị không đổi.
1) Chứng minh DF song song với AE.
2) Chứng minh rằng: BD.BE + AM.AD có giá trị không đổi.
a) Tứ giác BDFN nội tiếp nên \(\widehat{CNA}=\widehat{BDF}\) (*)
Xét đường tròn (K), đường kính BM, ta có \(\widehat{MNB}=90^o\) hay \(MN\perp AB\) tại N (1)
Với lí do tương tự, ta có \(AD\perp EB,BC\perp EA\), do đó M là trực tâm của tam giác EAB \(\Rightarrow EM\perp AB\) (2)
Từ (1) và (2) \(\Rightarrow\) M, N, P thẳng hàng và đường thẳng này vuông góc với AB.
Từ đó suy ra tứ giác BECN nội tiếp (vì \(\widehat{ECB}=\widehat{ENB}=90^o\))
\(\Rightarrow\widehat{CNA}=\widehat{AEB}\) (**)
Từ (*) và (**), suy ra \(\widehat{BDF}=\widehat{BEA}\) \(\Rightarrow\) DF//AE (đpcm)
b) Tương tự như trên, ta có tứ giác AEDN nội tiếp \(\Rightarrow\widehat{BND}=\widehat{AEB}\), dẫn đến \(\Delta BDN~\Delta BAE\left(g.g\right)\) \(\Rightarrow\dfrac{BD}{BA}=\dfrac{BN}{BE}\Rightarrow BD.BE=BA.BN\) (3)
Tứ giác NBMD nội tiếp nên \(\widehat{ANM}=\widehat{ADB}\), dẫn đến \(\Delta AMN~\Delta ABD\left(g.g\right)\)
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{AN}{AD}\Rightarrow AD.AM=AB.AN\) (4)
Cộng theo vế (3) và (4), thu được \(BD.BE+AM.AD=AB.BN+AB.AN=AB\left(BN+AN\right)=AB^2=4R^2\)không thay đổi. (đpcm)
Đúng 2
Bình luận (0)
cho tam giác ABC nội tiếp đường tròn tâm (o), đường kính AB2R trên cạnh BC lấy điểm M ( M khác B và C) đường thẳng AM cắt đường tròn O tại D, đường thẳng BD cắt AC tại E đường tròn tâm I ngoại tiếp tam giác MDB cắt đường kính ad tại điểm thứ hai là N1) chứng minh tứ giác CEDM nội tiếp đường tròn và 3 điểm E,M,N thẳng hàng2)cho đoạn thẳng CN cắt đường tròn(i) ở F .cmr : DF//AE
Đọc tiếp
cho tam giác ABC nội tiếp đường tròn tâm (o), đường kính AB=2R trên cạnh BC lấy điểm M ( M khác B và C) đường thẳng AM cắt đường tròn O tại D, đường thẳng BD cắt AC tại E đường tròn tâm I ngoại tiếp tam giác MDB cắt đường kính ad tại điểm thứ hai là N
1) chứng minh tứ giác CEDM nội tiếp đường tròn và 3 điểm E,M,N thẳng hàng
2)cho đoạn thẳng CN cắt đường tròn(i) ở F .cmr : DF//AE
1: góc ACB=góc ADB=1/2*sđ cung AB=90 độ
=>AC vuông góc CB và AD vuông góc DB
=>góc ECM=90 độ=góc EDM
=>CEDM nội tiếp
AC vuông góc CB
AD vuông góc DB
=>AD,BC là 2 đường cao của ΔAEB
=>M là trực tâm
=>AM vuông góc AB
ΔMDB vuông tại D nên ΔMDB nội tiếp đường tròn đường kính MB
=>BM là đường kính của (I)
=>góc MNB=90 độ
=>MN vuông góc AB
=>E,M,N thẳng hàng
b: AM vuông góc AB
=>góc ANM=90 độ
góc ANM+góc ACM=180 độ
=>ACMN nội tiếp
=>góc CAM=góc CNM=góc ADF
=>góc CAM=góc ADF
=>DF//AB
Đúng 0
Bình luận (0)
Cho tam giác ABC nội tiếp đường tròn tâm O đường kính AB= 2R. Trên cạnh BC lấy M ( M khác B và C), đường thẳng AM cắt (O ) ở D, E là giao điểm của BD và AC. Vẽ đường tròn (I ) ngoại tiếp tam giác MBD cắt đường kính AB ở N ( N khác B).
1. CMR: Tứ giác CEDM nội tiếp và 3 điểm E, M, N thẳng hàng 2,cho đoạn thẳng CN cắt đường tròn (i) ở F (giúp mình với ạ )
1: góc ECM+góc EDM=180 độ
=>ECMD nội tiếp
góc MNB=1/2*180=90 độ
EM vuông góc AB
MN vuông góc AB
=>E,M,N thẳng hàng
2: Đề bài yêu cầu gì?
Đúng 0
Bình luận (0)
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm (O). Trên cạnh BC lấy điểm D sao cho đường thẳng vuông góc với BC tại D cắt cung nhỏ AC tại đường tròn tâm (O) tại M. Gọi E là hình chiếu của M trên AC.
a) Chứng minh tứ giác CDEM nội tiếp một đường tròn.
b) Chứng minh: MA.MD=MB.ME.
a: góc CDM=góc CEM=90 độ
=>CDEM nội tiếp
b: Xet ΔMEA vuông tại E và ΔMDB vuông tại D có
góc EMA chung
=>ΔMEA đồng dạng với ΔMDB
=>ME/MD=MA/MB
=>ME*MB=MA*MD
Đúng 0
Bình luận (0)
a. góc CDM=góc CEM=90 độ
=>CDEM nội tiếp
b. Xet ΔMEA vuông tại E và ΔMDB vuông tại D có
góc EMA chung
=>ΔMEA đồng dạng với ΔMDB
=>ME/MD=MA/MB
=>ME*MB=MA*MD
Đúng 0
Bình luận (0)
1)Cho tam giác nhọn ABC (ABAC) nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC, K là giao điểm thứ hai của AH với đường tròn (O). Đường thẳng đi qua H và vuông góc với OA cắt BC ở I. Chứng minh rằng IK là tiếp tuyến của đường tròn (O)2)Cho tam giác ABC (ABAC) nội tiếp đường tròn (O), đường trung tuyến AM. Lấy điểm D trên cung BC không chứa A sao cho góc BAD góc CAM. Chứng minh góc ADB góc CDM3)Cho tam giác ABC nội tiếp đường tròn O tại D. Đường tròn (D;DB) cắt đường thẳng AB tại Q (k...
Đọc tiếp
1)Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC, K là giao điểm thứ hai của AH với đường tròn (O). Đường thẳng đi qua H và vuông góc với OA cắt BC ở I. Chứng minh rằng IK là tiếp tuyến của đường tròn (O)
2)Cho tam giác ABC (AB<AC) nội tiếp đường tròn (O), đường trung tuyến AM. Lấy điểm D trên cung BC không chứa A sao cho góc BAD= góc CAM. Chứng minh góc ADB= góc CDM
3)Cho tam giác ABC nội tiếp đường tròn O tại D. Đường tròn (D;DB) cắt đường thẳng AB tại Q (khác B), cắt đuòng thẳng AC tại P (khác C). Chứng minh rằng AO vuông góc PQ
Các bạn giúp mình nhé để mình làm cho xong bài tập kẻo xuân này con không về
1)Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC, K là giao điểm thứ hai của AH với đường tròn (O). Đường thẳng đi qua H và vuông góc với OA cắt BC ở I. Chứng minh rằng IK là tiếp tuyến của đường tròn (O)
~~~~~~~~~ Bài làm ~~~~~~~~~
Ta có: \(\widehat{HBD}=\widehat{DAC}\) (Cùng phụ với \(\widehat{ACB}\))
\(\widehat{KBD}=\widehat{DAC}\)( Góc nối tiếp cùng chắn cung \(KC\))
\(\Rightarrow\widehat{HBD}=\widehat{KBD}\)
Ta lại có: \(BD\perp HK\)
\(\Rightarrow BD\) là đường trung trực của \(HK\)
\(\Rightarrow\Delta IHK\) cân tại \(I\)
\(\Rightarrow\widehat{BKD}=\widehat{BHD}=\widehat{AHQ}\)
Lại có:\(\widehat{DKO}=\widehat{HAO}\)( \(\Delta OKA\) cân tại \(O\))
Vì vậy: \(\widehat{DKO}+\widehat{BKD}=\widehat{HAO}+\widehat{AHQ}=90^0\)
\(\Rightarrow\widehat{KIO}=90^0\)
\(\Rightarrow IK\)là tiếp tuyến của đường tròn \(\left(O\right)\)
(Hình vẽ chỉ mang tính chất minh họa cái hình vẽ gần cả tiếng đồng hồ :)) )
Ủa bạn ơi sao phụ nhau? Dòng đầu ấy
Đúng rồi bạn. Phụ nhau ý nghĩa là ^HBD + ^ACB = 90^0 và tương tự như góc kia. (Tam giác vuông ý)
Xem thêm câu trả lời
Cho tam giác ABc , lấy D trên cạnh BC , vẽ đường tròn tâm I qua D tiếp xúc với AB tại B. Vẽ đường tròn tâm K qua D tiếp xúc với AC tại C . Gọi M là giao điểm của hai đường tròn đó
1. CM : tứ giác ABMC nội tiếp
2. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC . CM : 3 đường tròn tâm I, tâm K và tâm O đồng quy
3. CM : MD di chuyển qua 1 điểm cố định
Cho tam giác ABC nội tiếp đường tròn (O),
AB < AC. Tia phân giác của góc A cắt BC ở D, cắt
đường tròn ở E. Trên tia AC lấy điểm K sao cho AK
= AB. Chứng minh rằng:
a) ∆ABD = ∆AKD
b) DKCE là tứ giác nội tiếp
BÀI 1 cho tam giác ABC vuông tại A .Nữa đường tròn đường kính AB cắt BC tại D.Trên cung AD lấy một điểm E .Nối BE và kéo dài AC tại F.Chứng minh tứ giác CDEF nội tiếp BÀI 2: Cho đường tròn tâm O đường kính AB cố định ,CD là đường kính thay đổi của đường tròn (O) ( khác AB ) .Tiếp tuyến tại B của (O ) cắt AC và AD lần lượt tại N và M .Chứng minh tứ giác CDMN nội tiếp BÀI 3 :Cho hai đoạn thẳng MN và PQ cắt nhau tại O .Biết OM.ON PO.OQ.Chứng minh tứ giác MNPQ nội tiếp BÀI 4: Cho tam giác ABC có đườ...
Đọc tiếp
BÀI 1 cho tam giác ABC vuông tại A .Nữa đường tròn đường kính AB cắt BC tại D.Trên cung AD lấy một điểm E .Nối BE và kéo dài AC tại F.Chứng minh tứ giác CDEF nội tiếp
BÀI 2: Cho đường tròn tâm O đường kính AB cố định ,CD là đường kính thay đổi của đường tròn (O) ( khác AB ) .Tiếp tuyến tại B của (O ) cắt AC và AD lần lượt tại N và M .Chứng minh tứ giác CDMN nội tiếp
BÀI 3 :Cho hai đoạn thẳng MN và PQ cắt nhau tại O .Biết OM.ON= PO.OQ.Chứng minh tứ giác MNPQ nội tiếp
BÀI 4: Cho tam giác ABC có đường cao AH . Gọi M, N lần lượt là hình chiếu vuông góc của H lên các cạnh AB, AC
a) c/m AMHN nội tiếp
b) BMNC nội tiếp
BÀI 5: Cho tam giác ABC các đường phân giác trong là BE và CF cắt nhau tại M và các đường phân giác ngoài của các góc B và góc C cắt nhau tại N .chứng minh BMCN nội tiếp
BÀI 6: Cho đường tròn (O) đường kính AB .Gọi M là một điểm trên tiếp tuyến xBy , đường thẳng AM cắt đường tròn (O) tại C , lấy D thuộc BM, nối AD cắt (O) tại I. c/m CIDM nội tiếp
BÀI 7: Cho đường tròn tâm (O) có cung EH và S là điểm chính giữa cung đó .Trên dây EH lấy hai điểm A và B .Các đường thẳng SA và SB cắt đường tròn lần lượt tại D và C .c/m ABCD là tứ giác nội tiếp
BÀI 8: Cho đường tròn (O) đường kính AB , từ A và B vẽ Ax vuông góc AB và By vuông góc BA (Ax và By cùng phía so với bờ AB ) .Vẽ tiếp tuyến x'My' (tiếp điểm M) cắt Ax tại C và By tại D ; OC cắt AM tại I và OD cắt BM tại K .Chứng minh CIKD nội tiếp
Cho tam giác abc vuông tại a . Trên cạnh ac lấy điểm d, rồi vẽ đường tròn tâm o nhận cd làm đường kính. Bd cắt đường tròn o tại e và ae cắt (o) tại f
a) tức giác abce nội tiếp
b)ad.dc=bd.de
c) giác acb= góc ace
d) lấy điểm m đối xứnv với d qua a. Điểm n đối xứng với d qua đường thẳng bc . Cm tứ giác bmcn nội tiếp được trong 1 đường tròn
Xem chi tiết
giải hộ em với ah
giảo cho em con d với ạ
















