Tại 3 đỉnh của tam giác ABC vuông tại A cạnh BC = 50 cm ; AC = 40 cm ; AB = 30 cm ta đặt các điện tích Q 1 = Q 2 = Q 3 = 10 - 9 C .Xác định cường độ điện trường tại H với H là chân đường cao kẻ từ
A. 400V/m
B. 246V/m
C. 254V/m
D. 175V/m
Tại 3 đỉnh của tam giác ABC vuông tại A cạnh BC = 50 cm, AC = 40 Cm, AB = 30 cm ta đặt các điện tích q1 = q2 = q3 = 10-9 C. Tìm độ lớn cường độ điện trường tại H là chân đường cao kẻ từ A.
A. 400 V/m
B. 246 V/m
C. 254 V/m
D. 175 V/m
Đáp án: B
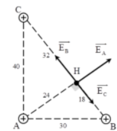
Áp dụng hệ thức lượng trong tam giác vuông ta tìm được: HC = 32cm, HB = 18cm, HA = 24 cm
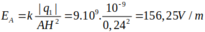
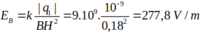
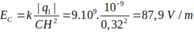
![]()
Cho tam giác ABC vuông tại A, tổng số đo của 2 cạnh góc vuông bằng 50 cm , cạnh AB bằng 2/3 cạnh AC .
A) Tính tam giác ABC
B) Từ điểm M cách A 10 cm, kẻ đường thẳng song song với AC cà cách BC tại N . Tính S hình thang AMNC.
CHO TAM GIÁC ABC CÓ AB=10, AC=24, BC=26
A)CM TAM GIÁC ABC LÀ TAM GIÁC VUÔNG
B) PHÂN GIÁC CỦA GÓC BAC VÀ PHÂN GIÁC CỦA GÓC NGOÀI TẠI ĐỈNH A CẮT ĐƯỜNG THẲNG BC LẦN LƯỢT TẠI D, E.TÍNH BD, CE VÀ ĐỘ DÀI CÁC CẠNH CỦA TAM GIÁC ADE
Cho hình tam giác ABC vuông tại đỉnh B và cạnh AB là 16,8 cm. Biết cạnh AB bằng 3 phần 5 cạnh BC . Tính diện tích hình tam giác.
cạnh BC là:
16,8 : 3/5 = 28
diện tích hình tam giác là:
16,8 x 28 : 2 = 235,2
Giải :
Cạnh BC là :
\(16,8\text{ : }\frac{3}{5}=28\text{ }\left(\text{cm}\right)\)
Diện tích tam giác là :
\(16,8\times28\text{ : }2=235,2\text{ }\left(\text{cm}^2\right)\)
Đáp số : 235,2 cm2
Tam giác ABC vuông cân tại A [AB = AC] có chu vi 126 cm, cạnh BC dài 50 cm. Tính diện tích tam giác ABC.
Tam giác ABC vuông cân tại A [AB = AC] có chu vi 126 cm, cạnh BC dài 50 cm. Tính diện tích tam giác ABC.
Tổng 2 cạnh goc vuông :
126 - 50 = 76 cm
Độ dài 1 cạnh goc vuông :
76 : 2 = 38 cm
DT tam giác ABC :
38 x 38 : 2 = 722 cm2
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC, H thuộc BC. Tia phân giác của góc H A B ^ cắt BC tại D, tia phân giác của góc H A C ^ cắt BC tại E. Chứng minh điểm cách đều ba cạnh của tam giác ABC chính là điểm cách đều ba đỉnh của tam giác ADE.
Cho Tam giác ABC vuông tại A , có AB=3 cm , BC= 5cm . Trên cạnh BC lấy điểm D sao cho BD= 3cm . Đường thẳng vuông góc với BC tại D cắt cạnh AC tại M , cắt tia BA tại N
a)Tính AC và so sánh các góc của tam giác ABC
b) Chứng minh MA=MD và tam giác MNC cân
c) Gọi I là trung điểm của CN . Chứng minh 3 điểm B,M,I thẳng hàng
a. Xét tam giác vuông ABC
Theo định lý Py - ta - go ta có :
AB2 + AC2 = BC2
=> 32 + AC2 = 52
=> 9 + AC2 = 25
=> AC2 = 16
=> AC = 4
Vậy AB < AC < BC
b. Xét tam giác BAM và tam giác BDM ta có :
BM chung
Góc BAM = góc BDM ( = 90 độ )
BA = BD ( gt)
=> tam giác BAM = tam giác BDM ( ch - cgv)
=> MA = MD ( hai cạnh tương ứng )
Xét tam giác AMN và tam giác DMC
góc AMN = góc DMC ( đối đỉnh )
MA = MD ( cmt)
góc MAN= góc MDC ( = 90 độ )
=> Tam giác AMN = tam giác DMC
=> MN = MC
=> Tam giác MNC cân
1. Cho tam giác ABC vuông tại A có AB = 9 cm , BC = 15 cm , AH là đường C10 ( H thuộc cạnh BC ) . Tính BH , CH , AC và AH ,
2. Cho tam giác ABC vuông tại A có AC = 5 cm , AB = 4 cm . Tính : a ) Cạnh huyền BC . b ) Hình chiếu của AB và AC trên cạnh huyền . c ) Đường cao AH .
3. Cho tam giác ABC vuông tại A có BC = 40 cm , AC = 36 cm . Tính AB , BH , CH và AH ,
4. Cho tam giác ABC vuông tại A có BC = 24 cm . Tính AB , AC , cho biết 2 AB = -AC .
5. Cho tam giác ABC vuông tại A có AH là đường cao . BH = 10 cm , CH = 42 cm . Tính BC , AH , AB và AC ,
6. Cho đường tròn tâm O bán kính R = 10 cm . A , B là hai điểm trên đường tròn ( O ) và I là trung điểm của đoạn thẳng AB . a ) Tính AB nếu OI = 7 cm . b ) Tính OI nếu AB = 14 cm .
Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=15^2-9^2=144\)
hay AC=12(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\\CH=\dfrac{12^2}{15}=\dfrac{144}{15}=9,6\left(cm\right)\end{matrix}\right.\)
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AH^2+HB^2=AB^2\)
\(\Leftrightarrow AH^2=9^2-5.4^2=51,84\)
hay AH=7,2(cm)