Cho tam giác ABCcó góc A < 90 độ .Vẽ phía ngoài tam giác ABC. Các tam giác vuông góc tại A,tam giác ABD, và tam giác ACE.biết AC=AE; AB=AD.Gọi I là trung diểm của BC.Chứng minh DE=2AI

Những câu hỏi liên quan
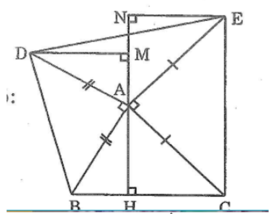
cho tam giác ABC . vẽ phía ngoài các tam giác ABC các tam giác vuông tại A là ABD , ACE có AB=AD , AC=AE. kẻ AH vuông góc vs BC , DM vuông góc vs AH , EN vuông góc vs AH
Cho tam giác ABC. Vẽ ở phía ngoài tam giác ABC các tam giác vuông tại A và ABD, ACE có AB = AD, AC = AE. Kẻ AH vuông góc với BC, DM vuông góc với AH, EN vuông góc với AH. Chứng minh rằng: DM = AH
Ta có: ∠(BAH) +∠(BAD) +∠(DAM) =180o(kề bù)
Mà ∠(BAD) =90o⇒∠(BAH) +∠(DAM) =90o(1)
Trong tam giác vuông AMD, ta có:
∠(AMD) =90o⇒∠(DAM) +∠(ADM) =90o(2)
Từ (1) và (2) suy ra: ∠(BAH) =∠(ADM)
Xét hai tam giác vuông AMD và BHA, ta có:
∠(BAH) =∠(ADM)
AB = AD (gt)
Suy ra: ΔAMD= ΔBHA(cạnh huyền, góc nhọn)
Vậy: AH = DM (hai cạnh tương ứng) (3)
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A nhọn, phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Gọi M là trung điểm của BC. Cm AM 1/2 DE và AM vuông góc DECho tam giác ABC có góc A nhọn, phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Gọi M là trung điểm của BC. Cm AM 1/2 DE và AM vuông góc DECho tam giác ABC có góc A nhọn, phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Gọi M là trung điểm của BC. Cm AM 1/2 DE và AM vuông góc DE
Đọc tiếp
Cho tam giác ABC có góc A nhọn, phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Gọi M là trung điểm của BC. Cm AM = 1/2 DE và AM vuông góc DECho tam giác ABC có góc A nhọn, phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Gọi M là trung điểm của BC. Cm AM = 1/2 DE và AM vuông góc DECho tam giác ABC có góc A nhọn, phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Gọi M là trung điểm của BC. Cm AM = 1/2 DE và AM vuông góc DE
Cho tam giác Abc, vẽ phía ngoài tam giác ABC các tam giác vuông tại A là tam giác ABD;tam giác ACE; có AB =AD; AC=AE. kẻ AH vuông góc BC; DM vuông góc ANH; EN vuông góc AH. chứng minh: a) DM = AH; b) MN đi qua trung điểm DE
Cho tam giác ABC ở phía ngoài tam giác ABC vẽ các tam giác vuông tại A đó là tam giác ABD và tam giác ACE có AB = AD và AC = AE Kẻ AH vuông góc BC Gọi I là giao điểm HA và DE . Chứng minh DI = IE
bài này mik chưa học mik mới lớp 6 thôi
Đúng 0
Bình luận (0)
hình tự vẽ nha bn!
kẻ EN vuông góc AH và DM vuông góc AH
ta có góc BAI=ABH+AHB ( góc ngoài bằng tổng 2 góc trong ko kề)
=> BAD+DAI=ABH+AHB
mà BAD=AHB (=90 độ)
=> góc DAI=ABH hay góc DAM=ABH
xét tam giác DAM vuông và tam giác vuong ABH có:DA=AB (gt),góc DAM=ABH
=> tam giác DAM=tam giác ABH (ch-gn) => DM=AH (1)
tương tự EN=AH (2)
(1),(2)=> DM=EN
ta có DM vuong góc AH,EN vuong góc AH=> DM//EN=> góc IDM=IEN
xét tam giác vuong DIM= tam giác vuong EIN (cgv-gnk)
=> DI=EI
Đúng 0
Bình luận (0)
Cho tam giác ABC, vẽ phía ngoài tam giác ABC các tam giác vuông tại A là: tam giác ABD và ACE có AB=AD, AC=AE. Kẻ AH vuông góc với BC, OM vuông góc với AH, EN vuông góc với AH. Chứng minh rằng:
a, Tam giác MAE = tam giác MCB
b, AE = À
c, Ba điểm A,E,F thẳng hàng
Cho tam giác ABC, vẽ phía ngoài tam giác ABC các tam giác vuông tại A là: tam giác ABD và ACE có AB=AD, AC=AE. Kẻ AH vuông góc với BC, OM vuông góc với AH, EN vuông góc với AH. Chứng minh rằng:
a, Tam giác MAE = tam giác MCB
b, AE = À
c, Ba điểm A,E,F thẳng hàng
Cho tam giác ABC ở phía ngoài tam giác vẽ các tam giác vuông tại A đó là tam giác ABD và tam giác ACE sao cho AB = AC và AC = AE . Kẻ AH vuông góc BC . Gọi I là giao điểm của HA và DE . Chứng minh DI = IE
xem lại chỗ đâm nhé
Cho tam giác ABC ở phía ngoài tam giác vẽ các tam giác vuông tại A đó là tam giác ABD và tam giác ACE sao cho AB = AC và AC = AE . Kẻ AH vuông góc BC . Gọi I là giao điểm của HA và DE . Chứng minh DI = IE
Đúng 0
Bình luận (0)
Cho tam giác ABC. Vẽ ở phía ngoài tam giác ABC các tam giác vuông tại A và ABD, ACE có AB = AD, AC = AE. Kẻ AH vuông góc với BC, DM vuông góc với AH, EN vuông góc với AH. Chứng minh rằng: MN đi qua trung điểm của DE
Ta có: ∠(HAC) +∠(CAE) +∠(EAN) =180o(kề bù)
Mà ∠(CAE) =90o⇒∠(HAC) +∠(EAN) =90o (4)
Trong tam giác vuông AHC, ta có:
∠(AHC) =90o⇒∠(HAC) +∠(HCA) =90o (5)
Từ (4) và (5) suy ra: ∠(HCA) =∠(EAN) ̂
Xét hai tam giác vuông AHC và ENA, ta có:
∠(AHC) =∠(ENA) =90o
AC = AE (gt)
∠(HCA) =∠(EAN) ( chứng minh trên)
Suy ra : ΔAHC= ΔENA(cạnh huyền, góc nhọn)
Vậy AH = EN (hai cạnh tương ứng)
Từ (3) và (6) suy ra: DM = EN
Vì DM ⊥ AH và EN ⊥ AH (giả thiết) nên DM // EN (hai đường thẳng cùng vuông góc với đường thẳng thứ ba)
Gọi O là giao điểm của MN và DE
Xét hai tam giác vuông DMO và ENO, ta có:
∠(DMO) =∠(ENO) =90o
DM= EN (chứng minh trên)
∠(MDO) =∠(NEO)(so le trong)
Suy ra : ΔDMO= ΔENO(g.c.g)
Do đó: DO = OE ( hai cạnh tương ứng).
Vậy MN đi qua trung điểm của DE
Đúng 0
Bình luận (0)


















