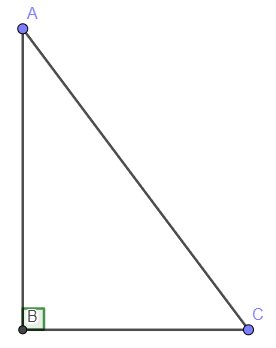
a, \(sin\left(A\right)=\dfrac{BC}{AC}\Leftrightarrow sin\left(40^o\right)=\dfrac{BC}{8}\Leftrightarrow BC\approx5,14\left(cm\right)\)
\(cos\left(A\right)=\dfrac{AB}{AC}\Leftrightarrow cos\left(40^o\right)=\dfrac{AB}{8}\Leftrightarrow AB\approx6,12\left(cm\right)\)
b,
\(cotg\left(C\right)=\dfrac{BC}{AB}\Leftrightarrow\dfrac{1}{\sqrt{3}}=\dfrac{BC}{5}\Leftrightarrow BC=\dfrac{5\sqrt{3}}{3}\left(cm\right)\)
\(AC^2=AB^2+BC^2\Leftrightarrow AC=\sqrt{AB^2+BC^2}=\sqrt{5^2+\left(\dfrac{5\sqrt{3}}{3}\right)^2}=\dfrac{10\sqrt{3}}{3}\left(cm\right)\)

Với $\Delta ABC$ có ˆA=90oA^=90o và ˆB=30oB^=30o

⇒ˆC=60o⇒C^=60o

Gọi $M$ là trung điểm của $BC$

Mà $\Delta ABC$ có ˆA=90oA^=90o

$\Rightarrow AM=BM=CM$ ( định lý)

$\Rightarrow \Delta AMC$ cân tại $M$

Mà ˆC=60oC^=60o

$\Rightarrow \Delta AMC$ đều

Ta có \(AC^2=CH.BC=AB.BC\)

Mà \(BC^2=AB^2+AC^2\) \(=AB^2+AB.BC\)

\(\Leftrightarrow AB^2+AB.BC-BC^2=0\)

\(\Leftrightarrow\left(\dfrac{AB}{BC}\right)^2+\dfrac{AB}{BC}-1=0\)

\(\Leftrightarrow\dfrac{AB}{BC}=\dfrac{-1+\sqrt{5}}{2}\)  (loại TH \(\dfrac{AB}{BC}=\dfrac{-1-\sqrt{5}}{2}< 0\))

\(\Leftrightarrow\cos B=\dfrac{\sqrt{5}-1}{2}\), đpcm.

a: Ta có: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC^2=5^2+12^2=169\)

=>\(BC=\sqrt{169}=13\left(cm\right)\)

Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{5}{13}\)

nên \(\widehat{B}\simeq23^0\)

Ta có: ΔABC vuông tại A

=>\(\widehat{B}+\widehat{C}=90^0\)

=>\(\widehat{C}\simeq90^0-23^0=67^0\)

b: Ta có: ΔABC vuông tại A

=>\(\widehat{B}+\widehat{C}=90^0\)

=>\(\widehat{C}=90^0-40^0=50^0\)

Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}\)

=>\(BC=\dfrac{AC}{sinB}=\dfrac{5}{sin40}\simeq7,78\left(cm\right)\)

ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(AB^2=BC^2-AC^2\)

=>\(AB\simeq\sqrt{7,78^2-5^2}\simeq5,96\left(cm\right)\)

Tương tự câu 1

a.

Áp dụng hệ thức lượt trong tam giác vuông ta có:

$\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}$

$\Leftrightarrow \frac{1}{AC^2}=\frac{1}{AH^2}-\frac{1}{AB^2}=\frac{1}{3a^2}$

$\Rightarrow AC=\sqrt{3}a$

$BC=\sqrt{AB^2+AC^2}=\sqrt{a^2+3a^2}=2a$

b.

$HB=\frac{BC}{4}$ thì $HC=\frac{3}{4}BC$

$\Rightarrow \frac{HB}{HC}=\frac{1}{3}$

Áp dụng hệ thức lượt trong tam giác vuông:

$AB^2=BH.BC; AC^2=CH.BC$

$\Rightarrow \frac{AB}{AC}=\sqrt{\frac{BH}{CH}}=\frac{\sqrt{3}}{3}$

Áp dụng định lý Pitago:

$4a^2=BC^2=AB^2+AC^2=(\frac{\sqrt{3}}{3}.AC)^2+AC^2$

$\Rightarrow AC=\sqrt{3}a$

$\Rightarrow AB=a$

c. 

Áp dụng hệ thức lượt trong tam giác vuông:

$AB^2=BH.BC$

$\Leftrightarrow AB^2=BH(BH+CH)$

$\Leftrightarrow a^2=BH(BH+\frac{3}{2}a)$

$\Leftrightarrow BH^2+\frac{3}{2}aBH-a^2=0$

$\Leftrightarrow (BH-\frac{a}{2})(BH+2a)=0$

$\Rightarrow BH=\frac{a}{2}$
$BC=BH+CH=2a$

$AC=\sqrt{BC^2-AB^2}=\sqrt{3}a$

d. Tương tự phần a.

Hình vẽ: