Để đo chiều cao của một cái cây người ta dựng hình vẽ và tiến hành đo đạc các đoạn B'C'=1,5m ; AB'=2m , B'B=8m. Tính chiều cao của cái cây.

Những câu hỏi liên quan
i 2: (1,5 điểm): Để đo chiều cao của một cây, người ta đã tiến hành cách đo và vẽ một bảng thiết kế như hình sau. Em hãy tính chiều cao của cây có độ dài A’C’, biết AC1,5m, BA2m, BA’16m và AC,A’C’ cùng vuông góc với A’B. Bài 3: (2,5 điểm) Cho tam giác ABC vuông tại A, AB 8cm, AC 6cm, AD là tia phân giác góc A,. a. Tính ? b. Kẻ đường cao AH (). Chứng minh rằng: . c.Tính
Đọc tiếp
i 2: (1,5 điểm):
Để đo chiều cao của một cây, người ta đã tiến hành cách đo và vẽ một bảng thiết kế như hình sau. Em hãy tính chiều cao của cây có độ dài A’C’, biết AC=1,5m, BA=2m, BA’=16m và AC,A’C’ cùng vuông góc với A’B.
Bài 3: (2,5 điểm) Cho tam giác ABC vuông tại A, AB = 8cm, AC = 6cm, AD là tia phân giác góc A,.
a. Tính ?
b. Kẻ đường cao AH ().
Chứng minh rằng: .
c.Tính
Có thể đo được chiều rộng của một khúc sông mà không cần phải sang bờ bên kia hay không ?
Người ta tiến hành đo đạc các yếu tố hình học cần thiết để tính chiều rộng của khúc sông mà không cần phải sang bờ bên kia (h.18). Nhìn hình vẽ đã cho, hãy mô tả những công việc cần làm và tính khoảng cách AB x theo BC a, BC a, BB h
Đọc tiếp
Có thể đo được chiều rộng của một khúc sông mà không cần phải sang bờ bên kia hay không ?
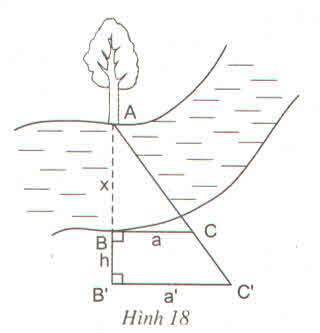
Người ta tiến hành đo đạc các yếu tố hình học cần thiết để tính chiều rộng của khúc sông mà không cần phải sang bờ bên kia (h.18). Nhìn hình vẽ đã cho, hãy mô tả những công việc cần làm và tính khoảng cách AB = x theo BC = a, B'C' = a', BB' = h
Ta có:
= mà AB' = x + h nên
= <=> a'x = ax + ah
<=> a'x - ax = ah
<=> x(a' - a) = ah
x=
Vậy khoảng cách AB bằng
Đúng 1
Bình luận (0)
Có thể đo dược chiều rông của một khúc sông mà không cần phải sang bờ bên kia hay không?
Người ta tiền hành đo đạc các yếu tố hình học cần thiết để tình chiều rộng của khúc sông mà không cần phải sang bờ bên kia(h18). Nhìn hình vẽ, Hãy mô tả những công việc cần làm và tính khoảng cách AB=x theo BC=a a, B'C'= a', BB'= h.
\
Ta có hình như sau :
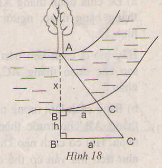
giải :
Ta có:
=
mà AB' = x + h nên
=
<=> a'x = ax + ah
<=> a'x - ax = ah
<=> x(a' - a) = ah
x=
Vậy khoảng cách AB bằng
Đúng 0
Bình luận (0)
Ta có hình như sau :

Giải
Ta có:
=
mà AB' = x + h nên
=
<=> a'x = ax + ah
<=> a'x - ax = ah
<=> x(a' - a) = ah
x=
Vậy khoảng cách AB bằng
Đúng 0
Bình luận (0)
Để đo chiều dài của cây bàng (đoạn AB) người ta dùng một cái cọc MN cao 1,5m đặt vuông góc với mặt đất có gắn thước ngắm sao cho hướng đi qua A của cây và 3 điểm A, M, C thẳng hàng. Người ta đo được khoảng cách từ C đến N là 1,2 và từ C đến B là 6m. Tính chiều cao của cây.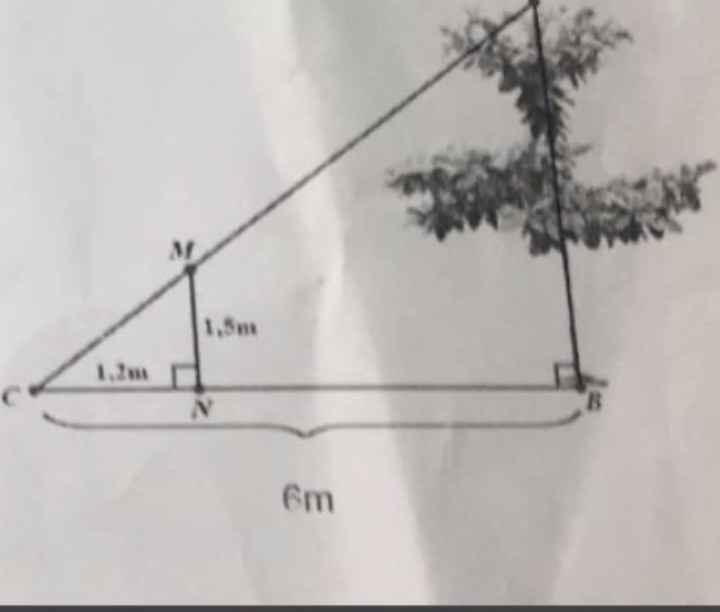
Ta có:MN\(\perp\)CB
AB\(\perp\)CB
Do đó: MN//AB
Xét ΔCAB có MN//AB
nên \(\dfrac{MN}{AB}=\dfrac{CN}{CB}\)
=>\(\dfrac{1.5}{AB}=\dfrac{1.2}{6}=\dfrac{1}{5}\)
=>AB=1,5*5=7,5(m)
Đúng 0
Bình luận (0)
Có thể đo được chiều rộng của một khúc sông mà không cần phải sang bờ bên kia hay không? Người ta tiến hành đo đạc các yếu tố hình học cần thiết để tính chiều rộng của khúc sông mà không cần phải sang bờ bên kia. Nhìn hình vẽ đã cho, hãy mô tả những công việc cần làm và tính khoảng cách AB x theo BC a, B’C’ a’; BB’ h.
Đọc tiếp
Có thể đo được chiều rộng của một khúc sông mà không cần phải sang bờ bên kia hay không?
Người ta tiến hành đo đạc các yếu tố hình học cần thiết để tính chiều rộng của khúc sông mà không cần phải sang bờ bên kia. Nhìn hình vẽ đã cho, hãy mô tả những công việc cần làm và tính khoảng cách AB =x theo BC =a, B’C’ = a’; BB’ = h.
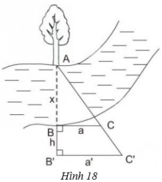
+ Mô tả cách làm:
- Chọn một điểm A cố định bên mép bờ sông bên kia (chẳng hạn như là một thân cây), đặt hai điểm B và B' thẳng hàng với A, điểm B sát mép bờ còn lại và AB chính là khoảng cách cần đo.
- Trên hai đường thẳng vuông góc với AB' tại B và B' lấy C và C' thằng hàng với A.
- Đo độ dài các đoạn BB' = h, BC = a, B'C' = a' ta sẽ tính được đoạn AB.
+ Cách tính AB.
Ta có: BC ⊥ AB’ và B’C’ ⊥ AB’ ⇒ BC // B’C’
ΔAB’C’ có BC // B’C’ (B ∈ AB’, C ∈ AC’)
⇒ 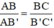 (hệ quả định lý Talet)
(hệ quả định lý Talet)
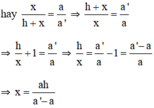
Đúng 0
Bình luận (0)
Có thể đo gián tiếp chiều cao của một bức tường khá cao bằng dụng cụ đơn giản được không? Hình 19 thể hiện cách đo chiều cao AB của một bức tường bằng các dụng cụ đơn giản gồm: Hai cọc thẳng đứng (cọc 1 cố định; cọc 2 có thể di động được) và sợi dây FC. Cọc 1 có chiều cao DK h. Các khoảng cách BC a, DC b đo được bằng thước dây thông dụng. a) Em hãy cho biết người ta tiến hành đo đạc như thế nào. b) Tính chiều cao AB theo h, a, b.
Đọc tiếp
Có thể đo gián tiếp chiều cao của một bức tường khá cao bằng dụng cụ đơn giản được không?
Hình 19 thể hiện cách đo chiều cao AB của một bức tường bằng các dụng cụ đơn giản gồm: Hai cọc thẳng đứng (cọc 1 cố định; cọc 2 có thể di động được) và sợi dây FC. Cọc 1 có chiều cao DK = h. Các khoảng cách BC = a, DC = b đo được bằng thước dây thông dụng.
a) Em hãy cho biết người ta tiến hành đo đạc như thế nào.
b) Tính chiều cao AB theo h, a, b.
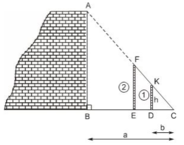
a) Cách tiến hành:
- Đặt hai cọc thẳng đứng, di chuyển cọc 2 sao cho 3 điểm A, F, K nằm trên đường thẳng.
- Dùng sợi dây căng thẳng qua 2 điểm F và K để xác định điểm C trên mặt đất (3 điểm F, K, C thẳng hàng).
b) ΔABC có AB // KD (D ∈ BC, K ∈ AC)
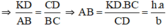
Vậy chiều cao bức tường là 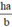
Đúng 0
Bình luận (0)
1) Để xác định chiều rộng của một khúc sông,người ta tiến hành đo đạc như hình vẽ bên.Hãy tính chiều rộng x của khúc sông, biết:a 10(m); a 14(m) và h 6(m)2) Cho AABC có đường phân giác AD.a) Giả sử AB 6cm, BC 10cm, AC 9cm, tính độ dài đoạn thắng BD.b) Trên tia đối của các tia AB và AC, lần lượt lấy các điểm E và F sao choAE AB, AC 3AF. Chứng minh EF // BC, từ đó suy ra AAEF AABC.3
Đọc tiếp
1) Để xác định chiều rộng của một khúc sông,
người ta tiến hành đo đạc như hình vẽ bên.
Hãy tính chiều rộng x của khúc sông, biết:
a = 10(m); a' = 14(m) và h = 6(m)
2) Cho AABC có đường phân giác AD.
a) Giả sử AB = 6cm, BC = 10cm, AC = 9cm, tính độ dài đoạn thắng BD.
b) Trên tia đối của các tia AB và AC, lần lượt lấy các điểm E và F sao cho
AE = AB, AC = 3AF. Chứng minh EF // BC, từ đó suy ra AAEF AABC.
3
người ta dự định bắc một cái cầu qua một con sông. Để đo khoảng cách giữa hai đầu A và B của cầu kĩ sư làm như sau. Một người đứng ở vị trí A, một người đứng ở vị trí C dọc trên cùng một bờ và tiến hành đo đạc. Kết quả đo được là khoảng cách AC=25m, góc BAC= 59 độ, góc BCA= 82 độ. Em hãy giúp kĩ sư tính khoảng cách giữa hai đầu cầu nhé
Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
=>\(\widehat{ABC}+59^0+82^0=180^0\)
=>\(\widehat{ABC}=39^0\)
Xét ΔABC có \(\dfrac{AC}{sinB}=\dfrac{AB}{sinC}\)
=>\(\dfrac{25}{sin39}=\dfrac{AB}{sin82}\)
=>\(AB=25\cdot\dfrac{sin82}{sin39}\simeq39,34\left(m\right)\)
Đúng 0
Bình luận (0)
Một nhà toán học muốn ước lượng chiều rộng của một cái hồ. Ông ta đánh dấu 5 điểm gần hồ và dùng kỹ thuật đo đạc để có được các số liệu như hình vẽ bên (tính theo đơn vị mét). Biết QR song song ST, hỏi chiều rộng của hồ (đoạn PQ) là bao nhiêu mét? Giải thích. (làm tròn đến chữ số thập phân thứ nhất)














