Cho lăng trụ đứng ABCD.A'B'C'D' có đáy là hı̀nh thoi cạnh 3a, góc B A D = 120 ° ; A A ' = 3 a Tı́nh thể tı́ch khối lăng trụ đã cho
A. 2 3 a 3
B. 27 3 a 3 2
C. 40 3 a 3
D. a 3 3
Cho lăng trụ đứng ABCD.A'B'C'D' có đáy là hı̀nh thoi cạnh 3a, góc B A D ^ = 120 0 . Tı́nh thể tı́ch khối lăng trụ đã cho
A . 2 3 a 3
B . 27 3 a 3 2
C . 40 3 a 3
D . 3 a 3
Đáp án là B
Ta có đáy là hı̀nh thoi có một góc
120
0
nên diện tı́ch đáy bằng 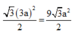
do lăng trụ đứng nên ta có thể tı́ch khối lăng trụ bằng 27 3 a 3 2
Cho hình lăng trụ đứng tam giác ABC.A'B'C' có đáy là \(\Delta\) vuông.có hai cạnh đáy góc vuông là AB=12cm và AC=8cm chiều cao hình lăng trụ là CC'=10cm tính Sxq.
\(S_{Xq}=\left(12+8+\sqrt{12^2+8^2}\right)\cdot10=\left(20+4\sqrt{13}\right)\cdot10\left(cm^2\right)\)
một lăng trụ đứng có đáy là 1 tam giác vuông, chiều cao lăng trụ là 7cm. Độ dài 2 cạnh góc vuông của đáy là 3cm; 4cm.Hãy tính :
a)Diện tích mặt đáy,
b)Diện tích xung quanh,
c)Thể tích lăng trụ
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A có BC = 2a. Biết góc giữa hai mặt phẳng (A'BC) và (ABC) bằng 60 ∘ và khoảng cách giữa hai đường thẳng A'A, BC bằng a 3 2 . Tính thể tích lăng trụ ABC.A'B'C'
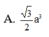
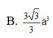
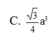
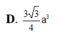
Cho hình lăng trụ đứng ABC.A’B’C’ có mặt đáy là tam giác ABC vuông tại B và AB=a ,BC =2a ,AA’=3a .Một mp(P) đi qua A và vuông góc với CA’ lần lượt cắt các đoạn thẳng CC’ và BB’ tại M và N . Tính S∆AMN.
1. Tính diện tích toàn phần của hình lăng trụ đứng có đáy là tam giác vuông cân, cạnh góc vuông là a, chiều cao 2a.
2.Chứng minh bất đẳng thức sau:
\(\left(2a+2b\right)\left(\dfrac{1}{4a}+\dfrac{1}{4b}\right)\ge2\) ( a, b > 0 )
1.
Cạnh huyền là: \(\sqrt{2a^2}\)
=> Chu vi đáy = \(2a+\sqrt{2a^2}\)
=> Sxq = \(2a\left(2a+\sqrt{2a^2}\right)\)
=> Stp = \(a^2+2a\left(2a+\sqrt{2a^2}\right)\)(đvdt)
p/s: Hình như là k rút gọn đc
2. Đề sai k ạ ? Tui lm k ra = 2, nếu mà đề đúng thì tui 0 biet lam
Cho lăng trụ đứng ABC A'B'C' có đáy ABC vuông cân tại B biết A'C = a và A'C hợp với mặt bên (AA'B'B) một góc 30 độ. Tính thể tích lăng trụ?
Cho hı̀nh chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD), đáy là hình thang ABCD vuông tại A và B có AB=a, AD=3a, BC=a. Biết SA=a 3 . Tính thể tích khối chóp S.BCD theo a.
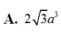
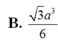
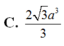
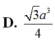
Cho lăng trụ đứng ABC.A’B’C’, đáy ABC là tam giác vuông cân tại A. E là trung điểm của B’C’, CB’ cắt BE tại M. Tính thể tích V của khối tứ diện ABCM biết AB = 3a, AA’ = 6a.
A. V = 7 a 3 .
B. V = 6 2 a 3 .
C. V = 8 a 3 .
D. V = 6 a 3 .