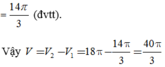Những câu hỏi liên quan
Cho đường tròn (O; R). Một đường thẳng d cắt đường tròn (O) tại hai điểm C và D. Từ một điểm I thuộc đường thẳng d, ở ngoài đường tròn (O) sao cho ID IC, kẻ hai tiếp tuyến IA và IB tới đường tròn (O). Gọi H là trung điểm của CD.1. Chứng minh năm điểm A, H, O, B, I cùng thuộc một đường tròn.2. Giả sử AI AO, khi đó tứ giác AOBI là hình gì? Tính diện tích hình tròn ngoại tiếp tứ giác AOBI? 3. Chứng minh rằng khi I di chuyển trên đường thẳng d thỏa mãn: Ở ngoài (O) và ID IC thì AB luôn đi qu...
Đọc tiếp
Cho đường tròn (O; R). Một đường thẳng d cắt đường tròn (O) tại hai điểm C và D. Từ một điểm I thuộc đường thẳng d, ở ngoài đường tròn (O) sao cho ID > IC, kẻ hai tiếp tuyến IA và IB tới đường tròn (O). Gọi H là trung điểm của CD.
1. Chứng minh năm điểm A, H, O, B, I cùng thuộc một đường tròn.
2. Giả sử AI = AO, khi đó tứ giác AOBI là hình gì? Tính diện tích hình tròn ngoại tiếp tứ giác AOBI?
3. Chứng minh rằng khi I di chuyển trên đường thẳng d thỏa mãn: Ở ngoài (O) và ID > IC thì AB luôn đi qua một điểm cố định.
1) Trong (O) có CD là dây cung không đi qua (O) và H là trung điểm CD
\(\Rightarrow OH\bot CD\Rightarrow\angle OHI=90=\angle OAI\Rightarrow OHAI\) nội tiếp
Ta có: \(\angle OAI+\angle OBI=90+90=180\Rightarrow OAIB\) nội tiếp
\(\Rightarrow O,H,A,B,I\) cùng thuộc 1 đường tròn
2) Vì IA,IB là tiếp tuyến \(\Rightarrow IB=IA=OA=OB\Rightarrow AOBI\) là hình thoi
có \(\angle OAI=90\Rightarrow AOBI\) là hình vuông
AB cắt OI tại E.Dễ chứng minh được E là trung điểm AB
Ta có: \(AB=\sqrt{OA^2+OB^2}=\sqrt{2}R\Rightarrow AE=\dfrac{\sqrt{2}}{2}R\)
\(\Rightarrow\) bán kính của (AOBI) là \(\dfrac{\sqrt{2}}{2}R\)
\(\Rightarrow\) diện tích của (AOBI) là \(\left(\dfrac{\sqrt{2}}{2}R\right)^2.\pi=\dfrac{1}{2}\pi R^2\)
3) OH cắt AB tại F
Ta có: \(\angle IEF=\angle IHF=90\Rightarrow IEHF\) nội tiếp
\(\Rightarrow OH.OF=OE.OI\) (cái này chỉ là đồng dạng thôi,bạn tự chứng minh nha)
mà \(OE.OI=OB^2=R^2\Rightarrow OF=\dfrac{R^2}{OH}\)
mà H cố định \(\Rightarrow\) F cố định \(\Rightarrow AB\) đi qua điểm F cố định 
Đúng 0
Bình luận (0)
Cho hai đường tròn
O
1
;
5
và
O
2
;
3
cắt nhau tại hai điểm A, B sao cho AB là một đường kính của đường tròn
O
2
. Gọi (D) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần gạch chéo...
Đọc tiếp
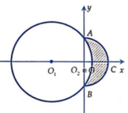
Cho hai đường tròn O 1 ; 5 và O 2 ; 3 cắt nhau tại hai điểm A, B sao cho AB là một đường kính của đường tròn O 2 . Gọi (D) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần gạch chéo như hình vẽ). Quay (D) quanh trục O 1 O 2 ta được một khối tròn xoay. Tính thể tích V của khối tròn xoay được tạo thành
A. V = 14 π 3
B. V = 68 π 3
C. V = 40 π 3
D. V = 36 π
Cho hai đường tròn
O
1
;
5
và
O
2
;
3
cắt nhau tại hai điểm A, B sao cho AB là một đường kính của đường tròn
O
2
. Gọi (D) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn...
Đọc tiếp
Cho hai đường tròn O 1 ; 5 và O 2 ; 3 cắt nhau tại hai điểm A, B sao cho AB là một đường kính của đường tròn O 2 . Gọi (D) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần gạch chéo như hình vẽ). Quay (D) quanh trục O 1 O 2 ta được một khối tròn xoay. Tính thể tích V của khối tròn xoay được tạo thành
A. V = 14 π 3
B. V = 68 π 3
C. V = 40 π 3
D. V = 36 π
Đáp án C

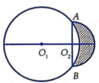
Chọn hệ tọa độ Oxy như hình vẽ với O 3 ≡ O , O 2 C ≡ O x , O 2 A ≡ O y .
Ta có
O 1 O 2 = O 1 A 2 − O 2 A 2 = 5 2 − 3 2 = 4 ⇒ O 1 − 4 ; 0 .
Phương trình đường tròn O 1 : x + 4 2 + y 2 = 25.
Phương trình đường tròn O 2 : x 2 + y 2 = 9.
Kí hiệu H 1 là hình phẳng giới hạn bởi các đường O 2 : x 2 + y 2 = 9, trục Oy: x = 0 khi x ≥ 0 .
Kí hiệu H 2 là hình phẳng giới hạn bởi các đường O 2 : x 2 + y 2 = 9, trục Oy: x=0 khi x ≥ 0 .
Khi đó thể tích V cần tìm chíình bằng thể tích V 2 của khối tròn xoay thu được khi quay hình H 2 xung quanh trục Ox (thể tích nửa khối cầu bán kính bằng 3) trừ đi thể tích V 1 của khối tròn xoay thu được khi quay hình H 1 xung quanh trục Ox.
Ta có V 2 = 1 2 . 4 3 π 3 3 = 18 π (đvtt);
V 1 = π ∫ 0 1 y 2 d x = π ∫ 0 1 25 − x + 4 2 d x = 14 π 3 (đvtt).
Vậy V = V 2 − V 1 = 18 π − 14 π 3 = 40 π 3 (đvtt).
Đúng 0
Bình luận (0)
Cho đường tròn (O) và đường thẳng (d) cắt đường tròn (O) tại hai điểm M; N ( đường thẳng (d) không đi qua O). Lấy điểm A thuộc đường thẳng (d) (A nằm ngoài đường tròn). Qua A kẻ hai tiếp tuyến AB và AC với đường tròn (B, C là tiếp điểm).a) Chứng minh đường tròn ngoại tiếp tam giác ABC luôn đi qua hai điểm cố định khi A di chuyển trên (d).b) Kẻ tiếp tuyến tại M và N của đường tròn (O) cắt nhau tại P. Chứng minh B; C; P thẳng hàng.c) Kẻ đường kính BOD, đường thẳng qua O vuông góc với BD cắt CD tại...
Đọc tiếp
Cho đường tròn (O) và đường thẳng (d) cắt đường tròn (O) tại hai điểm M; N ( đường thẳng (d) không đi qua O). Lấy điểm A thuộc đường thẳng (d) (A nằm ngoài đường tròn). Qua A kẻ hai tiếp tuyến AB và AC với đường tròn (B, C là tiếp điểm).a) Chứng minh đường tròn ngoại tiếp tam giác ABC luôn đi qua hai điểm cố định khi A di chuyển trên (d).b) Kẻ tiếp tuyến tại M và N của đường tròn (O) cắt nhau tại P. Chứng minh B; C; P thẳng hàng.c) Kẻ đường kính BOD, đường thẳng qua O vuông góc với BD cắt CD tại E. Chứng minh AOCE là hình thang cân
Cho hai đường tròn
O
1
;
5
và
O
2
;
3
cắt nhau tại hai điểm A, B sao cho AB là 1 đường kính của đường tròn
O
2
Gọi (D) là hình phẳng giới hạn bởi 2 đường tròn (ở ngoài đường tròn lớn, phần tô màu như hình vẽ)....
Đọc tiếp
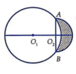
Cho hai đường tròn O 1 ; 5 và O 2 ; 3 cắt nhau tại hai điểm A, B sao cho AB là 1 đường kính của đường tròn O 2 Gọi (D) là hình phẳng giới hạn bởi 2 đường tròn (ở ngoài đường tròn lớn, phần tô màu như hình vẽ).Quay (D) quanh trục O 1 O 2 ta được một khối tròn xoay.Tính thể tích khối tròn xoay được tạo thành.

A. V=36π
B. V=68π/3
C. V=14π/3
D. V=40π/3
Cho đường tròn (O;R)và điểm A nằm ngoài đường tròn (O). Vẽ hai tiếp tuyến AB,AC của đường tròn (O)(B,C là hai tiếp điểm). Vẽ cát tuyến ADE của đường tròn (O) (D, E thuộc đường tròn (O); D nằm giữa A và E, tia AD nằm giữa hai tia AB,AO). Gọi I là trung điểm của DE và H là giao điểm của AO và BC.Chứng minh : góc EHO góc EDO
Đọc tiếp
Cho đường tròn (O;R)và điểm A nằm ngoài đường tròn (O). Vẽ hai tiếp tuyến AB,AC của đường tròn (O)(B,C là hai tiếp điểm). Vẽ cát tuyến ADE của đường tròn (O) (D, E thuộc đường tròn (O); D nằm giữa A và E, tia AD nằm giữa hai tia AB,AO). Gọi I là trung điểm của DE và H là giao điểm của AO và BC.
Chứng minh : góc EHO = góc EDO
Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC tại H
=>AH*AO=AB^2
Xet ΔABD và ΔAEB có
góc ABD=góc AEB
góc BAD chung
=>ΔABD đồng dạng với ΔAEB
=>AB^2=AD*AE=AH*AO
=>AD/AO=AH/AE
=>ΔADH đồng dạng với ΔAOE
=>góc ADH=góc AOE
=>góc DHO+góc DEO=180 độ
=>DEOH nội tiếp
=>góc EHO=góc EDO
Đúng 1
Bình luận (0)
Cho đường tròn (O, R), đường kính AB. Qua điểm A và điểm B lần lượt vẽ hai đường thẳng d và d’ là hai tiếp tuyến của đường tròn. Lấy điểm M bất kì thuộc đường tròn (O) (M khác A, B). Qua M kẻ tiếp tuyến với đường tròn (O) cắt d và d’ theo thứ tự tại C và D. a) Chứng minh A, C, M, O thuộc một đường tròn. b) Chứng minh AC.BD không đổi khi M di chuyển trên đường tròn (O)c) Chứng minh AB là tiếp tuyến của đường tròn ngoại tiếp DCOD.
Đọc tiếp
Cho đường tròn (O, R), đường kính AB. Qua điểm A và điểm B lần lượt vẽ hai đường thẳng d và d’ là hai tiếp tuyến của đường tròn. Lấy điểm M bất kì thuộc đường tròn (O) (M khác A, B). Qua M kẻ tiếp tuyến với đường tròn (O) cắt d và d’ theo thứ tự tại C và D.
a) Chứng minh A, C, M, O thuộc một đường tròn.
b) Chứng minh AC.BD không đổi khi M di chuyển trên đường tròn (O)
c) Chứng minh AB là tiếp tuyến của đường tròn ngoại tiếp DCOD.
a: Xét tứ giác ACMO có
\(\widehat{CAO}+\widehat{CMO}=90^0+90^0=180^0\)
=>ACMO là tứ giác nội tiếp
=>A,C,M,O cùng thuộc một đường tròn
b: Xét (O) có
CA,CM là các tiếp tuyến
Do đó: CA=CM và OC là phân giác của góc AOM
Xét (O) có
DM,DB là các tiếp tuyến
Do đó: DM=DB và OD là phân giác của góc MOB
OC là phân giác của góc AOM
=>\(\widehat{AOM}=2\cdot\widehat{MOC}\)
Ta có: OD là phân giác của góc MOB
=>\(\widehat{MOB}=2\cdot\widehat{MOD}\)
Ta có: \(\widehat{AOM}+\widehat{MOB}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{MOC}+2\cdot\widehat{MOD}=180^0\)
=>\(2\cdot\left(\widehat{MOC}+\widehat{MOD}\right)=180^0\)
=>\(2\cdot\widehat{COD}=180^0\)
=>\(\widehat{COD}=90^0\)
Xét ΔOCD vuông tại O có OM là đường cao
nên \(OM^2=MC\cdot MD\)
mà MC=CA và MD=DB
nên \(AC\cdot BD=OM=R^2\) không đổi
c: Gọi N là trung điểm của CD
Xét hình thang ACDB(AC//DB) có
O,N lần lượt là trung điểm của AB,CD
=>ON là đường trung bình của hình thang ABDC
=>ON//AC//BD
=>ON\(\perp\)AB
Vì ΔCOD vuông tại O có N là trung điểm của CD
nên N là tâm đường tròn ngoại tiếp ΔCOD
Xét (N) có
NO là bán kính
AB\(\perp\)NO tại O
Do đó: AB là tiếp tuyến của (N)
=>AB là tiếp tuyến của đường tròn ngoại tiếp ΔCOD
Đúng 1
Bình luận (0)
Cho hai đoạn thẳng AB và CD vuông góc với nhau (AB < AC).Vẽ đường tròn tâm O đường kính AB và đường tròn tâm O' đường kính AC.Gọi D là giao điểm thứ hai của hai đường tròn đó.
Chứng minh ba điểm B , D , C thẳng hàng
Cho đường tròn (C) tâm O bán kính R và hai đường thẳng d, e cắt mặt phẳng P của đường tròn (C) tại hai điểm A, B là hai đầu mút đường kính của đường tròn ấy. Đường thẳng d vuông góc với mặt phẳng P, d và e chéo nhau. M là một điểm tùy ý của đường tròn (C). Chứng minh rằng tồn tại một và chỉ một đường thẳng delta đi qua M và cắt d, e.
Đọc tiếp
Cho đường tròn (C) tâm O bán kính R và hai đường thẳng d, e cắt mặt phẳng P của đường tròn (C) tại hai điểm A, B là hai đầu mút đường kính của đường tròn ấy. Đường thẳng d vuông góc với mặt phẳng P, d và e chéo nhau. M là một điểm tùy ý của đường tròn (C). Chứng minh rằng tồn tại một và chỉ một đường thẳng delta đi qua M và cắt d, e.
Câu này còn 1 ý nữa, nên ý trên em không ra, em không biết giải ý dưới thế nào ạ!
b) Một mặt phẳng vuông góc với đường thẳng e cắt d, delta, e lần lượt ở A1, M1, B1. Chứng minh rằng tam giác A1M1B1 là vuông.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho đường tròn tâm O bán kính R và đường thẳng (d) cắt đường tròn tâm O tại hai điểm C và D (đường thẳng d không đi qua tâm O). Từ điểm S bất kì thuộc tia CD (S nằm ngoài đường tròn tâm O), kẻ hai tiếp tuyến SA và SB với đường tròn tâm O (với A và B là các tiếp điểm). Gọi H là trung điểm của đoạn CD và E là giao điểm của AB với SC. Chứng minh rằng: Khi S di chuyển trên tia CD (S nằm ngoài đường tròn tâm O) thì đường thẳng AB luôn đi qua 1 điểm cố định
Đọc tiếp
Cho đường tròn tâm O bán kính R và đường thẳng (d) cắt đường tròn tâm O tại hai điểm C và D (đường thẳng d không đi qua tâm O). Từ điểm S bất kì thuộc tia CD (S nằm ngoài đường tròn tâm O), kẻ hai tiếp tuyến SA và SB với đường tròn tâm O (với A và B là các tiếp điểm). Gọi H là trung điểm của đoạn CD và E là giao điểm của AB với SC. Chứng minh rằng: Khi S di chuyển trên tia CD (S nằm ngoài đường tròn tâm O) thì đường thẳng AB luôn đi qua 1 điểm cố định