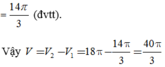Cho hai đường tròn (O; 2cm), (O’; 3cm), OO’ = 6cm. Tính độ dài BC

Những câu hỏi liên quan
Cho hai đường tròn (O) và (O') tiếp xúc ngoài ở A . Đường nối tâm OO' cắt đường tròn (O) ở B , cắt đường tròn (O') ở C . DE là tiếp tuyến chung ngoài của hai đường tròn , D thuộc (O) và E thuộc (O') . Gọi M là giao điểm của hai đường thẳng BD và CE . Chứng minh :
a) MA là tiếp tuyến chung của hai đường tròn (O) và (O')
b) MD.MB=ME.MC
Cho hai đường tròn (O) và (O) tiếp xúc ngoài ở A . Tiếp tuyến chung ngoài của hai đường tròn , tiếp xúc với đường tròn (O) ở M , tiếp xúc với đường tròn (O) ở N . Qua A kẻ đường vuông góc với OO cắt MN ở I a) Chứng minh tam giác AMN , IOO là tam giác vuông b) Chứng minh rằng MN là tiếp tuyến của đường tròn đường kính OO c) Cho biết OA8cm , OA 4,5cm . Tính độ dài MN
Đọc tiếp
Cho hai đường tròn (O) và (O') tiếp xúc ngoài ở A . Tiếp tuyến chung ngoài của hai đường tròn , tiếp xúc với đường tròn (O) ở M , tiếp xúc với đường tròn (O') ở N . Qua A kẻ đường vuông góc với OO' cắt MN ở I
a) Chứng minh tam giác AMN , IOO' là tam giác vuông
b) Chứng minh rằng MN là tiếp tuyến của đường tròn đường kính OO'
c) Cho biết OA=8cm , O'A =4,5cm . Tính độ dài MN
Cho hai đường tròn đồng tâm O. Dãy AB của đường tròn lớn cắt đường tròn nhỏ ở C và D. Chứng minh rằng AC = BD.
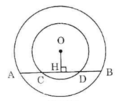
Giả sử vị trí các điểm theo thứ tự là A, C, B, D.
Kẻ OH ⊥ CD. Theo tính chất đường kính vuông góc với một dây ta có:
HA = HB, HC = HD
Nên AC = HA – HC = HB – HD = BD
Vậy AC = BD.
(Trường hợp vị trí các điểm theo thứ tự là A, D, C, B chứng minh tương tự.)
Đúng 0
Bình luận (0)
Cho hai đường tròn đồng tâm O. Dãy AB của đường tròn lớn cắt đường tròn nhỏ ở C và D. Chứng minh rằng AC = BD.
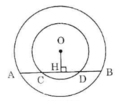
Giả sử vị trí các điểm theo thứ tự là A, C, B, D.
Kẻ OH ⊥ CD. Theo tính chất đường kính vuông góc với một dây ta có:
HA = HB, HC = HD
Nên AC = HA – HC = HB – HD = BD
Vậy AC = BD.
(Trường hợp vị trí các điểm theo thứ tự là A, D, C, B chứng minh tương tự.)
Đúng 0
Bình luận (0)
Cho hai đường tròn
O
1
;
5
và
O
2
;
3
cắt nhau tại hai điểm A, B sao cho AB là một đường kính của đường tròn
O
2
. Gọi (D) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần gạch chéo...
Đọc tiếp
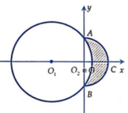
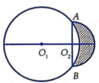
Cho hai đường tròn O 1 ; 5 và O 2 ; 3 cắt nhau tại hai điểm A, B sao cho AB là một đường kính của đường tròn O 2 . Gọi (D) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần gạch chéo như hình vẽ). Quay (D) quanh trục O 1 O 2 ta được một khối tròn xoay. Tính thể tích V của khối tròn xoay được tạo thành
A. V = 14 π 3
B. V = 68 π 3
C. V = 40 π 3
D. V = 36 π
Cho hai đường tròn
O
1
;
5
và
O
2
;
3
cắt nhau tại hai điểm A, B sao cho AB là một đường kính của đường tròn
O
2
. Gọi (D) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn...
Đọc tiếp
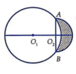
Cho hai đường tròn O 1 ; 5 và O 2 ; 3 cắt nhau tại hai điểm A, B sao cho AB là một đường kính của đường tròn O 2 . Gọi (D) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần gạch chéo như hình vẽ). Quay (D) quanh trục O 1 O 2 ta được một khối tròn xoay. Tính thể tích V của khối tròn xoay được tạo thành
A. V = 14 π 3
B. V = 68 π 3
C. V = 40 π 3
D. V = 36 π
Đáp án C

Chọn hệ tọa độ Oxy như hình vẽ với O 3 ≡ O , O 2 C ≡ O x , O 2 A ≡ O y .
Ta có
O 1 O 2 = O 1 A 2 − O 2 A 2 = 5 2 − 3 2 = 4 ⇒ O 1 − 4 ; 0 .
Phương trình đường tròn O 1 : x + 4 2 + y 2 = 25.
Phương trình đường tròn O 2 : x 2 + y 2 = 9.
Kí hiệu H 1 là hình phẳng giới hạn bởi các đường O 2 : x 2 + y 2 = 9, trục Oy: x = 0 khi x ≥ 0 .
Kí hiệu H 2 là hình phẳng giới hạn bởi các đường O 2 : x 2 + y 2 = 9, trục Oy: x=0 khi x ≥ 0 .
Khi đó thể tích V cần tìm chíình bằng thể tích V 2 của khối tròn xoay thu được khi quay hình H 2 xung quanh trục Ox (thể tích nửa khối cầu bán kính bằng 3) trừ đi thể tích V 1 của khối tròn xoay thu được khi quay hình H 1 xung quanh trục Ox.
Ta có V 2 = 1 2 . 4 3 π 3 3 = 18 π (đvtt);
V 1 = π ∫ 0 1 y 2 d x = π ∫ 0 1 25 − x + 4 2 d x = 14 π 3 (đvtt).
Vậy V = V 2 − V 1 = 18 π − 14 π 3 = 40 π 3 (đvtt).
Đúng 0
Bình luận (0)
Cho hai đường tròn (O,R) và (O',R') với R lớn hơn R' cắt nhau ở A và B sao cho O và O' ở về hai phía của AB. Vẽ tiếp tuyến AD với đường tròn (O). Qua B vẽ đường thẳng song song với AD cắt đường tròn (O') tại E và cắt đường tròn (O) tại F. CMR: Tứ giác ADEF là hbh
Cho đường tròn (O; R). Một đường thẳng d cắt đường tròn (O) tại hai điểm C và D. Từ một điểm I thuộc đường thẳng d, ở ngoài đường tròn (O) sao cho ID IC, kẻ hai tiếp tuyến IA và IB tới đường tròn (O). Gọi H là trung điểm của CD.1. Chứng minh năm điểm A, H, O, B, I cùng thuộc một đường tròn.2. Giả sử AI AO, khi đó tứ giác AOBI là hình gì? Tính diện tích hình tròn ngoại tiếp tứ giác AOBI? 3. Chứng minh rằng khi I di chuyển trên đường thẳng d thỏa mãn: Ở ngoài (O) và ID IC thì AB luôn đi qu...
Đọc tiếp
Cho đường tròn (O; R). Một đường thẳng d cắt đường tròn (O) tại hai điểm C và D. Từ một điểm I thuộc đường thẳng d, ở ngoài đường tròn (O) sao cho ID > IC, kẻ hai tiếp tuyến IA và IB tới đường tròn (O). Gọi H là trung điểm của CD.
1. Chứng minh năm điểm A, H, O, B, I cùng thuộc một đường tròn.
2. Giả sử AI = AO, khi đó tứ giác AOBI là hình gì? Tính diện tích hình tròn ngoại tiếp tứ giác AOBI?
3. Chứng minh rằng khi I di chuyển trên đường thẳng d thỏa mãn: Ở ngoài (O) và ID > IC thì AB luôn đi qua một điểm cố định.
1) Trong (O) có CD là dây cung không đi qua (O) và H là trung điểm CD
\(\Rightarrow OH\bot CD\Rightarrow\angle OHI=90=\angle OAI\Rightarrow OHAI\) nội tiếp
Ta có: \(\angle OAI+\angle OBI=90+90=180\Rightarrow OAIB\) nội tiếp
\(\Rightarrow O,H,A,B,I\) cùng thuộc 1 đường tròn
2) Vì IA,IB là tiếp tuyến \(\Rightarrow IB=IA=OA=OB\Rightarrow AOBI\) là hình thoi
có \(\angle OAI=90\Rightarrow AOBI\) là hình vuông
AB cắt OI tại E.Dễ chứng minh được E là trung điểm AB
Ta có: \(AB=\sqrt{OA^2+OB^2}=\sqrt{2}R\Rightarrow AE=\dfrac{\sqrt{2}}{2}R\)
\(\Rightarrow\) bán kính của (AOBI) là \(\dfrac{\sqrt{2}}{2}R\)
\(\Rightarrow\) diện tích của (AOBI) là \(\left(\dfrac{\sqrt{2}}{2}R\right)^2.\pi=\dfrac{1}{2}\pi R^2\)
3) OH cắt AB tại F
Ta có: \(\angle IEF=\angle IHF=90\Rightarrow IEHF\) nội tiếp
\(\Rightarrow OH.OF=OE.OI\) (cái này chỉ là đồng dạng thôi,bạn tự chứng minh nha)
mà \(OE.OI=OB^2=R^2\Rightarrow OF=\dfrac{R^2}{OH}\)
mà H cố định \(\Rightarrow\) F cố định \(\Rightarrow AB\) đi qua điểm F cố định 
Đúng 0
Bình luận (0)
Cho hai đường tròn đồng tâm O. Dây AB của đường tròn lớn cắn đường tròn nhỏ ở C vad D. Chứng minh rằng AC = BD
Hướng dẫn giải:
Vẽ OM⊥ABOM⊥AB.

Theo tính chất đường kính vuông góc với một dây ta được MA=MB và MC=MD.
Từ đó suy ra AC=BD.
Nhận xét. Kết luận bài toán vẫn được giữ nguyên nếu C và D đổi chỗ cho nhau.
Đúng 0
Bình luận (0)
Cho hai đường tròn đồng tâm O. Dây AB của đường tròn lớn cắt đường tròn nhỏ ở C và D. Chứng minh rằng AC=BD