Viết phương trình tiếp tuyến kẻ từ điểm A (2; 3) tới đồ thị hàm số y = 3 x + 4 x - 1
A. y = -28x+59; y = x+1
B. y = -24x+59; y = x+1
C. y = -28x+59
D. y = -28x+59; y = -24x+51
Viết phương trình tiếp tuyến kẻ từ điểm A (2; 3) tới đồ thị hàm số y = 3 x + 4 x - 1
A. y = -28x+59; y = x+1
B. y = -24x+51; y = x+1
C. y = -28x+59
D. y = -28x+59; y = -24x+51
- Ta có:
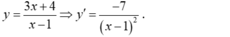
- Phương trình tiếp tuyến của đồ thị
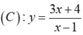
tại điểm M ( x 0 ; y 0 ) ∈ (C) với x0 ≠ 2 là:
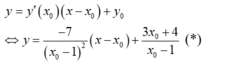
- Vì tiếp tuyến đi qua điểm A(2; 3) nên ta có:
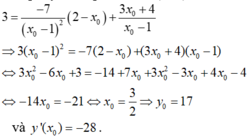
- Vậy có một tiếp tuyến thỏa đề bài là:
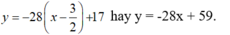
Chọn C.
Trong không gian Oxyz, cho mặt cầu ( S ) : x 2 + y 2 + ( z - 1 ) 2 = 4 và điểm A ( 2 ; 2 ; 1 ) . Từ điểm A kẻ ba tiếp tuyến AB, AC, AD với B, C, D là các tiếp điểm. Viết phương trình mặt phẳng ( B C D ) .
A . 2 x + 2 y + z - 1 = 0 .
B . 2 x + 2 y + z + 1 = 0 .
C . 2 x + 2 y + z - 3 = 0 .
D . 2 x + 2 y + z - 5 = 0 .
Trong không gian Oxyz, cho mặt cầu (S): x 2 + y 2 + ( z - 1 ) 2 = 4 và điểm A(2;2;1). Từ điểm A kẻ ba tiếp tuyến AB, AC, AD với B, C, D là các tiếp điểm. Viết phương trình mặt phẳng (BCD).
![]()
![]()
![]()
![]()
toan 10 cho đường tròn (c) (x-1)^2+(Y+1)^2=1 từ điểm M ( 3,4) kẻ đc hai tiếp tuyến của đường tròn, gọi A, B lần lượt là 2 tiếp điểm của đường tròn. hãy viết phương trình tổng quát của AB
Đường tròn (C) tâm \(I\left(1;-1\right)\) bán kính \(R=1\)
\(\Rightarrow\overrightarrow{IM}=\left(2;5\right)\Rightarrow IM=\sqrt{29}\)
Gọi H là trung điểm AB \(\Rightarrow IM\perp AB\) tại H \(\Rightarrow IH=d\left(I;AB\right)\)
Áp dụng hệ thức lượng trong tam giác vuông AIM:
\(IA^2=IH.IM\Rightarrow IH=\dfrac{R^2}{IM}=\dfrac{1}{\sqrt{29}}\)
Đường thẳng AB vuông góc IM nên nhận (2;5) là 1 vtpt
Phương trình AB có dạng: \(2x+5y+c=0\)
Do \(d\left(I;AB\right)=IH=\dfrac{1}{\sqrt{29}}\) \(\Rightarrow\dfrac{\left|2.1-5.1+c\right|}{\sqrt{2^2+5^2}}=\dfrac{1}{\sqrt{29}}\)
\(\Rightarrow\left|c-3\right|=1\Rightarrow\left[{}\begin{matrix}c=4\\c=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}2x+5y+2=0\\2x+5y+4=0\end{matrix}\right.\)
Mặt khác I và M nằm ở hai phía so với đường thẳng AB \(\Rightarrow\) đường thẳng có pt \(2x+5y+4=0\) không thỏa mãn do \(\left(2.3+5.4+4\right).\left(2.1-5.1+4\right)>0\)
Vậy pt đường thẳng AB là: \(2x+5y+2=0\)
Cho hàm số y = \(\dfrac{2x-1}{x-1}\) đồ thị (C). Viết phương trình tiếp tuyến của (C), biết rằng khoảng cách từ điểm I(1;2) đến tiếp tuyến bằng \(\sqrt{2}\) . Với điểm I như trên, viết phương trình tiếp tuyến của (C) để khoảng cách từ I đến tiếp tuyến Max
\(y'=\dfrac{-1}{\left(x-1\right)^2}\)
Gọi tiếp tuyến qua điểm \(M\left(a;b\right)\) thuộc (C) có dạng:
\(y=\dfrac{-1}{\left(a-1\right)^2}\left(x-a\right)+\dfrac{2a-1}{a-1}\)
\(\Leftrightarrow x+\left(a-1\right)^2y-2a^2+2a-1=0\)
Áp dụng công thức khoảng cách:
\(\dfrac{\left|1+2\left(a-1\right)^2-2a^2+2a-1\right|}{\sqrt{1+\left(a-1\right)^4}}=\sqrt{2}\)
\(\Leftrightarrow\left|2a-2\right|=\sqrt{2}.\sqrt{1+\left(a-1\right)^4}\)
\(\Leftrightarrow2\left(a-1\right)^2=1+\left(a-1\right)^4\)
\(\Leftrightarrow\left[\left(a-1\right)^2-1\right]^2=0\Rightarrow a=...\)
b.
Vẫn từ công thức khoảng cách trên:
\(d=\dfrac{\left|2a-2\right|}{\sqrt{1+\left(a-1\right)^4}}=\dfrac{2\sqrt{\left(a-1\right)^2}}{\sqrt{1+\left(a-1\right)^4}}=\dfrac{2}{\sqrt{\dfrac{1}{\left(a-1\right)^2}+\left(a-1\right)^2}}\)
\(d\le\dfrac{2}{\sqrt{2\sqrt{\dfrac{\left(a-1\right)^2}{\left(a-1\right)^2}}}}=\sqrt{2}\)
Vậy \(d_{max}=\sqrt{2}\) khi tiếp tuyến trùng với các tiếp tuyến câu a
Cho A (1,-1) B(2,-2)C(3,0) a) viết phương trình tổng quát AB,AC,BC b) viết phương trình các đường cao AH. Tìm tọa độ h c) viết phương trình tổng quát đường cao AH trung tuyến kẻ từ a,b,c d) viết phương trình đường tròn ngoại tiếp tam giác abc
a: vecto AB=(1;-1); vecto AC=(2;1); vecto BC=(1;2)
AB có VTPT là (1;1)
Phương trình AB là;
1(x-1)+1(y+1)=0
=>x+y=0
AC có VTPT là (-1;2)
PT AC là:
-1(x-1)+2(y+1)=0
=>-x+1+2y+2=0
=>-x+2y+3=0
BC có VTPT là (-2;1)
PT BC là;
-2(x-2)+1(y+2)=0
=>-2x+y+6=0
b: AH có VTPT là (1;2)
Phương trình AH là:
1(x-1)+2(y+1)=0
=>x-1+2y+2=0
=>x+2y+1=0
Viết phương trình tiếp tuyến kẻ từ M(3;1) đến đường tròn: (C) x 2 + y 2 - 4x + 2y + 2 = 0
* Xét đường tròn (C): x 2 + y 2 - 4x + 2y + 2 = 0
ta có: 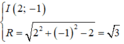
* Phương trình đường thẳng Δ kẻ từ M(3; 1) có dạng:
a(x - 3) + b(y - 1) = 0 ⇔ ax - 3a + by - b = 0 ⇔ ax + by - 3a - b = 0
* Vì đường thẳng Δ là tiếp tuyến của đường tròn (C) nên ta có:
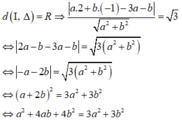
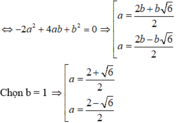


Vậy phương trình tiếp tuyến kẻ từ M(3;1) đến đường tròn (C): x 2 + y 2 - 4x + 2y + 2 = 0 là:
(2 + 6 )x + 2y - 8 - 3 6 = 0 hoặc (2 - 6 )x + 2y - 8 + 3 6 = 0
Cho đường tròn (C) có phương trình x 2 + y 2 − 4 x + 2 y − 4 = 0 . Một phương trình tiếp tuyến của đường tròn kẻ từ điểm M(-4; 2) là
A. – 4x + 3y – 22 = 0
B. 4x + 3y + 10 = 0
C. 3x + 4y + 4 = 0
D.3x – 4y +20 = 0
ĐÁP ÁN B
Đường tròn (C): x 2 + y 2 - 4 x + 2 y – 4 = 0 có tâm I(2; -1) và bán kính R = 2 2 + ( − 1 ) 2 + 4 = 3
Tiếp tuyến qua M( -4; 2) và nhận n → ( a ; b ) làm VTPT có phương trình :
a( x+ 4) + b (y – 2)= 0 hay ax + by + 4a – 2b = 0 (*)
Khoảng cách từ tâm I đến tiếp tuyến bằng bán kính nên ta có:
d ( I ; d ) = R ⇔ 2 a − b + 4 a − 2 b a 2 + b 2 = 3 ⇔ 6 a − 3 b a 2 + b 2 = 3 ⇔ 2 a − b a 2 + b 2 = 1 ⇔ 2 a − b = a 2 + b 2 ⇔ 4 a 2 − 4 a b + b 2 = a 2 + b 2 ⇔ 3 a 2 − 4 a b = 0 ⇔ a ( 3 a − 4 b ) = 0 ⇔ a = 0 3 a = 4 b
* Nếu a= 0 , chọn b= 1 thay vào (*) ta có phương trình tiếp tuyến là: y – 2= 0
* Nếu 3a = 4b, chọn a = 4 thì b = 3 thay vào (*) ta có phương trình tiếp tuyến là:
4x + 3y + 10 = 0
Vậy có 2 tiếp tuyến qua M là: y – 2= 0 và 4x +3y + 10= 0
Viết phương trình đường tròn qua A (1,1) và tiếp xúc với trục tung tại điểm H(0,-2) . Viết phương trình tiếp tuyến tại điểm A