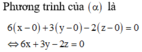Hãy viết phương trình mặt phẳng ( α ) đi qua gốc tọa độ O(0; 0; 0) và song song với mặt phẳng ( β ) : x + y + 2z – 7 = 0.

Những câu hỏi liên quan
Cho hai mặt phẳng
α
:
3
x
-
2
y
+
2
z
+
7
0
,
β
:
5
x
-
4
y
+
3...
Đọc tiếp
Cho hai mặt phẳng α : 3 x - 2 y + 2 z + 7 = 0 , β : 5 x - 4 y + 3 z + 1 = 0 . Phương trình mặt phẳng đi qua gốc tọa độ O đồng thời vuông góc với cả α và β là:
A. 2x - y - 2z =0
B. 2x - y + 2z =0
C. 2x + y - 2z + 1=0
D. 2x + y - 2z = 0
Đáp án D
Gọi mặt phẳng cần tìm là (P). Khi đó (P) nhận vtpt của α và β là cặp vtcp
![]()
![]()
![]()
Đúng 0
Bình luận (0)
Cho hai mặt phẳng
α
:
3
x
-
2
y
+
2
z
+
7
0
,
β
:
5
x
-
4
y
+
3
z
+
1
0
.
Phương trình mặt phẳng đi qua gốc tọa độ O đồng thời vuông góc với cả
(
α
)
và
β
là: A...
Đọc tiếp
Cho hai mặt phẳng α : 3 x - 2 y + 2 z + 7 = 0 , β : 5 x - 4 y + 3 z + 1 = 0 . Phương trình mặt phẳng đi qua gốc tọa độ O đồng thời vuông góc với cả ( α ) và β là:
A. 2 x - y - 2 z = 0
B. 2 x - y + 2 z = 0
C. 2 x + y - 2 z + 1 = 0
D. 2 x + y - 2 z = 0
Cho điểm
M
−
2
;
1
;
1
. Viết phương trình mặt phẳng
α
đi qua gốc tọa độ
O
0
;
0
;
0
và cách M một khoảng lớn nhất A.
x
−
y
+
z
0...
Đọc tiếp
Cho điểm M − 2 ; 1 ; 1 . Viết phương trình mặt phẳng α đi qua gốc tọa độ O 0 ; 0 ; 0 và cách M một khoảng lớn nhất
A. x − y + z = 0
B. − x + 2 y − z = 0
C. − 2 x + y + z = 0
D. 2 x − y − 2 z = 0
Cho điểm
M
-
2
;
1
;
1
. Viết phương trình mặt phẳng
α
đi qua gốc tọa độ
O
0
;
0
;
0
và cách M một khoảng lớn nhất. A.
x
-
y
+
z
0
B....
Đọc tiếp
Cho điểm M - 2 ; 1 ; 1 . Viết phương trình mặt phẳng α đi qua gốc tọa độ O 0 ; 0 ; 0 và cách M một khoảng lớn nhất.
A. x - y + z = 0
B. - x + 2 y - z = 0
C. - 2 x + y + z = 0
D. x - y - 2 z = 0
Đáp án C
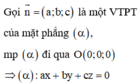
Khoảng cách từ M đến mặt phẳng α bằng:
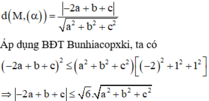
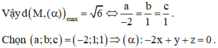
Đúng 0
Bình luận (0)
Trong không gian Oxyz, mặt phẳng
(
α
)
đi qua gốc tọa độ O(0;0;0) và có vectơ pháp tuyến là
n
⇀
(
6
;
3
;
-
2
)
thì phương trình của
(
α
)
là A.
-
6
x
+
3
y
-
2
0
B.
6...
Đọc tiếp
Trong không gian Oxyz, mặt phẳng ( α ) đi qua gốc tọa độ O(0;0;0) và có vectơ pháp tuyến là n ⇀ = ( 6 ; 3 ; - 2 ) thì phương trình của ( α ) là
A. - 6 x + 3 y - 2 = 0
B. 6 x - 3 y - 2 z = 0
C . - 6 x - 3 y - 2 z = 0
D. 6 x + 3 y - 2 z = 0
Trong không gian Oxyz, mặt phẳng
α
đi qua gốc tọa độ O (0;0;0) và có vectơ pháp tuyến là
n
→
6
;
3
;
-
2
thì phương trình của
α
là A.
-
6
x
+
3
y
-
2...
Đọc tiếp
Trong không gian Oxyz, mặt phẳng α đi qua gốc tọa độ O (0;0;0) và có vectơ pháp tuyến là n → = 6 ; 3 ; - 2 thì phương trình của α là
A. - 6 x + 3 y - 2 z = 0
B. 6 x - 3 y - 2 z = 0
C. - 6 x - 3 y - 2 z = 0
D. 6 x + 3 y - 2 z = 0
Trong không gian Oxyz, mặt phẳng
α
đi qua gốc tọa độ O(0;0;0) và có vectơ pháp tuyến là
n
→
(
6
;
3
;
-
2
)
thì phương trình của
α
là: A. -6x+3y-2z0. B. 6x-3y-2z0. C. -6x-3y-2z0. D. 6x+3y-2z0.
Đọc tiếp
Trong không gian Oxyz, mặt phẳng α đi qua gốc tọa độ O(0;0;0) và có vectơ pháp tuyến là n → = ( 6 ; 3 ; - 2 ) thì phương trình của α là:
A. -6x+3y-2z=0.
B. 6x-3y-2z=0.
C. -6x-3y-2z=0.
D. 6x+3y-2z=0.
Trong không gian Oxyz mặt phẳng
α
đi qua gốc tọa độ O và có vec-tơ pháp tuyến
n
⇀
6
;
3
;
-
2
thì phương trình của
α...
Đọc tiếp
Trong không gian Oxyz mặt phẳng α đi qua gốc tọa độ O và có vec-tơ pháp tuyến n ⇀ = 6 ; 3 ; - 2 thì phương trình của α là
A. -6x + 3y -2z = 0
B. 6x - 3y -2z = 0
C. -6x - 3y - 2z = 0
D. 6x + 3y - 2z = 0
Chọn đáp án D
Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng α đi qua gốc tọa độ O 0 ; 0 ; 0 luôn có phương trình dạng A x + B y + C z = 0 với n ⇀ = A ; B ; C A 2 + B 2 + C 2 # 0 là một vec-tơ pháp tuyến của mặt phẳng đó.
Tổng quát: Phương trình mặt phẳng đi qua điểm M x o ; y o ; z o và nhận n ⇀ = A ; B ; C A 2 + B 2 + C 2 # 0 làm một vec-tọa độ pháp tuyến thì có phương trình tổng quát được viết theo công thức
A x - x o + B y - y o + C z - z o = 0
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz cho điểm
M
1
;
0
;
6
và mặt phẳng
α
có phương trình là
x
+
2
y
+
2
z
−
1
0
. Viết phương trình mặt phẳng
β
đi qua M và song song với
α
A.
β...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho điểm M 1 ; 0 ; 6 và mặt phẳng α có phương trình là x + 2 y + 2 z − 1 = 0 . Viết phương trình mặt phẳng β đi qua M và song song với α
A. β : x + 2 y + 2 z + 13 = 0.
B. β : x + 2 y + 2 z − 15 = 0.
C. β : x + 2 y + 2 z − 13 = 0.
D. β : x + 2 y + 2 z + 15 = 0.