Hàm số nào sau đây đồng biến trên − ∞ ; + ∞
A. y = x 4 + 2 x 2
B. y = − x 3 + 3 x − 2
C. y = x 3 + 1
D. y = x x + 1
Hàm số nào sau đây là hàm số đồng biến trên ℝ ?
A. 3 2 a 3
B. 3 3 3 a 3
C. 3 4 a 3
D. 3 3 4 a 3
Hàm số nào trong các hàm số sau đây đồng biến trên R
A. y = x 2 - 2 x + 3
B. y = x 3 + x
C. y = 1 + 1 ( x 2 + 1 )
D. y = l n ( x 2 + 1 )
Cho hàm số f(x) có đạo hàm f ' x = x + 1 2 x − 1 3 2 − x . Hàm số f(x) đồng biến trên khoảng nào dưới đây?
A. 2 ; + ∞
B. (-1;1)
C. (1;2)
D. − ∞ ; − 1
Đáp án C
f ' x > 0 ⇔ 1 < x < 2 ⇒ hàm số đồng biến trên khoảng (1;2)
Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập số thực R ?
A. y = π 3 x
B. y = log 1 2 x
C. y = log π 4 2 x 2 + 1
D. y = 2 e x
Hàm số y = x 4 - 2 x 2 - 1 đồng biến trên khoảng nào sau đây
A. ( - 1 ; 0 ) ; ( 1 ; + ∞ )
B. Đồng biến trên ℝ
C. ( - ∞ ; - 1 ) ; ( 0 ; 1 )
D. ( - 1 ; 0 ) ; ( 0 ; 1 )
Cho hàm số f(x) có bẳng biến thiên như sau

Hàm số đã cho nghịch biến trong khoảng nào dưới đây?
A. 2 ; + ∞
B. - 1 ; 2
C. - ∞ ; - 1
D. - 2 ; 1
Đáp án B
Quan sát bảng biến thiên ta thấy trong khoảng (-1;2) hàm số có f'(x)<0 nên nghịch biến trong khoảng (-1;2)
Cho hàm số \(y=\dfrac{x^3}{3}-x^2+x+2019\): Mệnh đề nào đúng?
A: Hàm số đã cho đồng biến trên R
B: Hàm số đã cho nghịch biến trên(-\(\infty\);1)
C: Hàm số đã cho đồng biên trên (-\(\infty\);1) và nghịch biến trên (1;+\(\infty\))
D: Hàm số đã cho đồng biến trên (1;+\(\infty\)) và nghịch biên trên(-\(\infty\);1)
\(y'=x^2-2x+1=\left(x-1\right)^2\ge0\) ;\(\forall x\in R\)
\(\Rightarrow\) Hàm đồng biến trên R
Bảng biến thiên trong hình vẽ dưới đây là bảng biến thiên của hàm số nào?
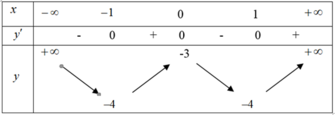
A. y = -x4 + 2x2 – 3
B. y = x4 – 2x2 – 3
C. y = -x4 + x2 – 3
D. y = x4 + 2x2 – 3
Đáp án B.
Thay x = -1 vào hàm số y = x4 – 2x2 – 3 ta có y(-1) = (-1)4 – 2(-1)2 – 3 = -4. Vậy hàm số này thỏa mãn bảng biến thiên bên trên
Cho hàm số y = f x có bảng biến thiên như sau
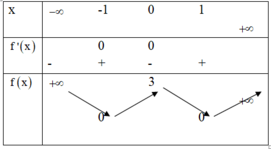
Mêṇh đề nào dưới đây là mêṇh đề sai?
A. Hàm số có hai điểm cực tiểu bằng 0.
B. Hàm số có hai điểm cực tiểu.
C. Hàm số có giá trị cực đại bằng 3.
D. Hàm số có ba điểm cực trị.