Cho z 1 = 1 + i ; z 2 = 2 - 2 i . Viết z 1 z 2 dưới dạng lượng giác?
A. 2 2 cos - π 2 + i . sin - π 2
B. 2 2 cos - π 4 + i . sin - π 4
C. 2 2 cos π 4 + i . sin π 4
D. 2 2 cos π 2 + i . sin π 2
Những câu hỏi liên quan
Cho
z
∈
C
thỏa mãn
(
2
+
i
)
|
z
|
10
z
+
1
-
2
i
. Tìm giá trị của biểu thức T|z+1+i|+|z-(1+i)|
Đọc tiếp
Cho z ∈ C thỏa mãn ( 2 + i ) | z | = 10 z + 1 - 2 i . Tìm giá trị của biểu thức T=|z+1+i|+|z-(1+i)|
Cho số phức z thỏa mãn ( 2 + i ) z + 2 ( 1 + 2 i ) 1 + i . Môđun của số phức w = z + i + 1 là
A. 3
B. 4
C. 5
D. 6
Cho số phức z thỏa mãn
(
2
z
-
1
)
(
1
+
i
)
+
(
z
¯
+
1
)
(
1
-
i
)
2
-
2
i
. Giá trị của |z| là ? A.
2
3...
Đọc tiếp
Cho số phức z thỏa mãn ( 2 z - 1 ) ( 1 + i ) + ( z ¯ + 1 ) ( 1 - i ) = 2 - 2 i . Giá trị của |z| là ?
A. 2 3
B. 2.
C. 3 2
D. 2 2
Cho số phức z thỏa mãn (1+z)(1+i)-5+i=0. Số phức w=1+z bằng
A. -1+3i.
B. 1-3i.
C. -2+3i.
D. 2-3i
Cho z = 3(1 + i) - 4(1-i). Tìm |z|
A. |z| = 5 2
B. |z| = 5
C. |z| = 7
D. |z| = 50
Cho số phức z 1+ ( 1+ i) + ( 1+i) 2+ ...+ (1+ i) 26 . Phần thực của số phức z là A.
2
13
B.
-
1
+
2
13
C.
-
2
13
D.
1
+
2
13
Đọc tiếp
Cho số phức z = 1+ ( 1+ i) + ( 1+i) 2+ ...+ (1+ i) 26 . Phần thực của số phức z là
A. 2 13
B. - 1 + 2 13
C. - 2 13
D. 1 + 2 13
Chọn A. Số phức z là tổng của cấp số nhân với số hạng đầu là 1 và công bội q = 1 + i. Do đó:
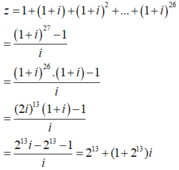
Vậy phần thực là: 213
Đúng 0
Bình luận (0)
Cho hai số phức z (2x+3) + (3y-1)i và z (y-1)i. Ta có z z khi:
A
.
x
3
2
;
y
0
B
.
x
-
3
2
;
y
0
C
.
x...
Đọc tiếp
Cho hai số phức z = (2x+3) + (3y-1)i và z' = (y-1)i. Ta có z = z' khi:
A . x = 3 2 ; y = 0
B . x = - 3 2 ; y = 0
C . x = 3 ; y = 1 3
D . x = 0 ; y = - 3 2
Câu 1: Tìm phần thực phần ảo của Z thỏa mãn 1+(1+i)+(1+i^2)+...+(1+i)^20
Câu 2: Tìm 1/Z sao cho Z=(3+căn3 i)^3
Câu 3: Tìm Z thỏa mãn môđun (Z-1)/(Z+1)=1 hoặc môđun (Z-3i)/(Z+1)=1
1/Áp dụng công thức tổng cấp số nhân:
\(z=1+\left(1+i\right)+\left(1+i\right)^2+...+\left(1+i\right)^{20}=1+\frac{\left(1+i\right)^{21}-1}{i+1-1}=1+\frac{\left(1+i\right)^{21}-1}{i}\)
Ta có:
\(\left(1+i\right)^{21}=\left(1+i\right)\left[\left(1+i\right)^2\right]^{10}=\left(1+i\right)\left(1+2i+i^2\right)^{10}\)
\(=\left(1+i\right)\left(2i\right)^{10}=\left(1+i\right).2^{10}.i^{10}=\left(1+i\right)2^{10}\left(i^2\right)^5=-\left(1+i\right).2^{10}\)
\(\Rightarrow z=1+\frac{-\left(1+i\right)2^{10}-1}{i}=1+\frac{-i\left(1+i\right)2^{10}-i}{i^2}=1+\left(i+i^2\right)2^{10}+i=1+i+\left(i-1\right).2^{10}\)
\(\Rightarrow z=\left(1-2^{10}\right)+\left(1+2^{10}\right)i\)
2/
\(z=\left(3+i\sqrt{3}\right)^3\Rightarrow\frac{1}{z}=\frac{1}{\left(3+i\sqrt{3}\right)^3}=\frac{\left(3-i\sqrt{3}\right)^3}{\left(3+i\sqrt{3}\right)^3\left(3-i\sqrt{3}\right)^3}=\frac{\left(3-i\sqrt{3}\right)^3}{\left(9-3i^2\right)^3}\)
\(\Rightarrow\frac{1}{z}=\frac{\left(3-i\sqrt{3}\right)^3}{12^3}=\left(\frac{1}{4}-\frac{\sqrt{3}}{12}i\right)^3\)
3/ Bạn viết lại đề được không?
Đúng 0
Bình luận (1)
cho số phức z thỏa mãn (1+i)z+\(\overline{z}\)=i . tìm mô- đun của số phức w= 1+i+z
tìm mô đum của số phức z biết z^2 (1-i) +2(\(\overline{z}\))^2 (1+i) = 21-i
bài 1) đặc \(z=a+bi\) với \(a;b\in z;i^2=-1\)
ta có : \(\left(1+i\right)z+\overline{z}=i\Leftrightarrow\left(1+i\right)\left(a+bi\right)+\left(a-bi\right)=i\)
\(\Leftrightarrow a-b+ai+bi+a-bi=i\Leftrightarrow2a-b+ai=i\)
\(\Leftrightarrow\left\{{}\begin{matrix}2a-b=0\\a=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\)
\(\Rightarrow z=1+2i\) \(\Rightarrow W=1+i+z=1+i+1+2i=2+3i\)
\(\Rightarrow\) \(modul\) của số phức \(W\) là : \(\left|W\right|=\sqrt{2^2+3^2}=\sqrt{13}\)
vậy .............................................................................................................
bài 2) đặc \(z=a+bi\) với \(a;b\in z;i^2=-1\)
ta có : \(z^2\left(1-i\right)+2\overline{z}^2\left(1+i\right)=21-i\)
\(\Leftrightarrow\left(a+bi\right)^2\left(1-i\right)+2\left(a-bi\right)^2\left(1+i\right)=21-i\)
\(\Leftrightarrow\left(a^2+2abi-b^2\right)\left(1-i\right)+2\left(a^2-2abi-b^2\right)\left(1+i\right)=21-i\)\(\Leftrightarrow a^2-a^2i+2abi+2ab-b^2+b^2i+2\left(a^2+a^2i-2abi+2ab-b^2-b^2i\right)=21-i\)
\(\Leftrightarrow a^2-a^2i+2abi+2ab-b^2+b^2i+2a^2+2a^2i-4abi+4ab-2b^2-2b^2i=21-i\)
\(\Leftrightarrow a^2-a^2i+2abi+2ab-b^2+b^2i+2a^2+2a^2i-4abi+4ab-2b^2-2b^2i=21-i\)\(\Leftrightarrow3a^2+6ab-3b^2+a^2i-2abi-b^2i=21-i\)
\(\Leftrightarrow\left(3a^2+6ab-3b^2\right)+\left(a^2-2ab-b^2\right)i=21-i\)
\(\Leftrightarrow\left\{{}\begin{matrix}3a^2+6ab-3b^2=21\\a^2-2ab-b^2=-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3a^2+6ab-3b^2=21\\3a^2-6ab-3b^2=-1\end{matrix}\right.\)
\(\Rightarrow-ab=-2\Leftrightarrow-a^2b^2=-4\) và \(a^2-b^2=3\)
\(\Rightarrow a^2\) và \(-b^2\) là nghiệm của phương trình \(X^2-3X-4=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2=4\\-b^2=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a^2=4\\b^2=1\end{matrix}\right.\)
\(\Rightarrow\) \(modul\) của số phức \(z\) là \(\left|z\right|=\sqrt{a^2+b^2}=\sqrt{4+1}=\sqrt{5}\)
vậy ...................................................................................................................
hôm sau phân câu 1 ; câu 2 rỏ ra nha bạn . cho dể đọc thôi 
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn điều kiện (1 - i)(2 + i)z + 1 - i = (5 - i)(1 + i). Tính môđun của số phức w = 1 + 2 z + z 2
A. 8
B. 64
C. 2 2
D. 5
Đáp án A
Ta có z = 5 - i 1 + i + i - 1 1 - i 2 + i = 1 + 2 i ⇒ w = 8 i ⇒ w = 8 .
Đúng 0
Bình luận (0)