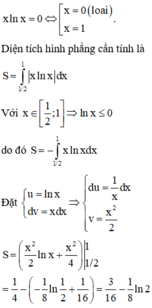Diện tích hình phẳng giới hạn bởi các đường y = x 3 ; y = - x ; x = 1
A. 4
B. 3 4
C. 1 4
D. 1
Những câu hỏi liên quan
Cho hình phẳng giới hạn bởi đồ thị các hàm số
y
x
, đường thẳng y 2 - x và trục hoành. Diện tích hình phẳng sinh bởi hình phẳng giới hạn bởi các đồ thị trên là A.
7
6
.
B.
4
3
.
C.
5
6
.
D.
5
4
.
Đọc tiếp
Cho hình phẳng giới hạn bởi đồ thị các hàm số y = x , đường thẳng y = 2 - x và trục hoành. Diện tích hình phẳng sinh bởi hình phẳng giới hạn bởi các đồ thị trên là
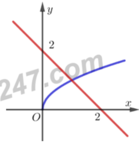
A. 7 6 .
B. 4 3 .
C. 5 6 .
D. 5 4 .
Diện tích miền hình phẳng giới hạn bởi các đường
y
2
x
, y -x+3, y 1 bằng A. . B. . C. . D. .
Đọc tiếp
Diện tích miền hình phẳng giới hạn bởi các đường y = 2 x , y = -x+3, y = 1 bằng
A. 
.
B. 
.
C. 
.
D. 
.
Biết diện tích hình phẳng giới hạn bởi đường cong yf(x), y0, x2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong yf(2x), trục hoành Ox và hai đường thẳng x0, xa bằng:
Đọc tiếp
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x), y=0, x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0, x=a bằng:
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x),y=0,x=0,x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0,x=a bằng
A. S/4.
B. 4S.
C. 2S.
D. S/2.
Tính diện tích hình phẳng giới hạn bởi các đường : y= x3- x và y= x- x2
A.12/9
B. 37/12
C.32/7
D.25/8
Đồ thị hàm số y = x3 - x; y = x - x2 .Đặt f1(x) = x3 - x, f2(x) = x - x2
Ta có f1(x) - f2(x) = 0 <=> x3 + x2 - 2x = 0 có 3 nghiệm x = -2; x = 0 ; x = 1
Vậy : Diện tích hình phẳng đã cho là :
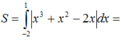
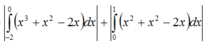
= 37 12
Đúng 0
Bình luận (0)
Tính diện tích hình phẳng được giới hạn bởi các đường
x
y
2
;
y
x
3
;
y
x
A
.
1
2
B
.
1
4
C
.
2
3...
Đọc tiếp
Tính diện tích hình phẳng được giới hạn bởi các đường x = y 2 ; y = x 3 ; y = x
A . 1 2
B . 1 4
C . 2 3
D . 1 3
Diện tích hình phẳng giới hạn bởi các đường
y
x
3
+
11
x
-
6
,
y
6
x
2
, x 0, x 2. (Đơn vị diện tích) A.
4
3
B.
5
2
C.
8
3
D.
18...
Đọc tiếp
Diện tích hình phẳng giới hạn bởi các đường y = x 3 + 11 x - 6 , y = 6 x 2 , x = 0, x = 2. (Đơn vị diện tích)
A. 4 3
B. 5 2
C. 8 3
D. 18 23
Chọn B.
Đặt h x = x 3 + 11 x - 6 - 6 x 2 = x 3 - 6 x 2 + 11 x - 6 h x = 0 ⇔ x = 1 ∨ x = 2 ∨ x = 3 ( l o ạ i )
Bảng xét dấu
Đúng 0
Bình luận (0)
Cho hình phẳng (H) giới hạn bởi các đường
y
xlnx
, trục hoành, đường thẳng
x
1
2
. Tính diện tích hình phẳng (H). A.
1
16
−
1
8
ln
2
B.
3
16
−
1
8
ln
2
C. ...
Đọc tiếp
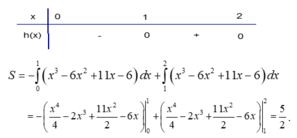
Cho hình phẳng (H) giới hạn bởi các đường y = xlnx , trục hoành, đường thẳng x = 1 2 . Tính diện tích hình phẳng (H).
A. 1 16 − 1 8 ln 2
B. 3 16 − 1 8 ln 2
C. 3 16 + 1 8 ln 2
D. 1 8 3 − ln 2
Đáp án B
Điều kiện: x > 0
Phương trình hoành độ giao điểm của đồ thị hàm số y=x.lnx và trục hoành là
Đúng 0
Bình luận (0)
Cho hình phẳng
H
giới hạn bởi các đường
y
x
ln
x
, trục hoành, đường thẳng
x
1
2
. Tính diện tích hình phẳng
H
. A.
1
8
3
-
ln
2
B.
3
16
-
1...
Đọc tiếp
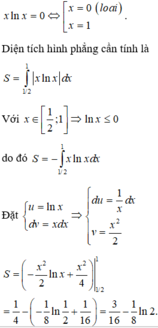
Cho hình phẳng H giới hạn bởi các đường y = x ln x , trục hoành, đường thẳng x = 1 2 . Tính diện tích hình phẳng H .
A. 1 8 3 - ln 2
B. 3 16 - 1 8 ln 2
C. 3 16 + 1 8 ln 2
D. 1 16 - 1 8 ln 2
Đáp án B
Điều kiện: x > 0
Phương trình hoành độ giao điểm của đồ thị hàm số và trục hoành là
Đúng 0
Bình luận (0)