Cho hình 1, biết: a ⊥ P Q ; b ⊥ P Q và N ^ = 75 0 .
Tính số đo x của góc M
Những câu hỏi liên quan
Bài 4:Cho hình vẽ, biết aperpMP tại M, bperp NQ tại Q, widehat{N_1}65^O.a) Chứng tỏ a//b.b) Tính widehat{M_1}? M P Q a b 1 1 65 độ N
Đọc tiếp
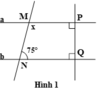
Bài 4:Cho hình vẽ, biết a\(\perp\)MP tại M, \(b\perp NQ\) tại Q, \(\widehat{N_1}\)=\(65^O\).
a) Chứng tỏ a//b.
b) Tính \(\widehat{M_1}\)=?
ta có : a \(\perp\) P và b \(\perp\) Q \(\Rightarrow\)a//b
M1 và N1 là cặp góc trong cùng phía bù nhau
\(\Rightarrow\)M1= \(^{180^0}\)- N1= 180- \(65^0\)= 115
Đúng 0
Bình luận (0)
1.Cho hình thang ABCD có 2 đáy AB và CD . Điểm M nằm trên nằm trên đoạn thẳng AC sao cho AM CM;điểm N trên cạnh CD sao cho MN song song với BD . Biết diện tích hình thang ABCD16cm2.a) CM : Diện tích hình tam giác BMN bằng diện tích hình tam giác DMNb) Tính diện tích hình tứ giác ABND 2.Cho Afrac{1}{1times101}+frac{1}{2cdot102}+....+frac{1}{25cdot125}Bfrac{1}{1cdot26}+frac{1}{2cdot27}+....+frac{1}{100cdot125}Tính frac{A}{B}Các bạn ơi giúp mk nhé !
Đọc tiếp
1.Cho hình thang ABCD có 2 đáy AB và CD . Điểm M nằm trên nằm trên đoạn thẳng AC sao cho AM = CM;điểm N trên cạnh CD sao cho MN song song với BD . Biết diện tích hình thang ABCD=16cm2.
a) CM : Diện tích hình tam giác BMN bằng diện tích hình tam giác DMN
b) Tính diện tích hình tứ giác ABND
2.Cho A=\(\frac{1}{1\times101}+\frac{1}{2\cdot102}+....+\frac{1}{25\cdot125}\)
B=\(\frac{1}{1\cdot26}+\frac{1}{2\cdot27}+....+\frac{1}{100\cdot125}\)
Tính \(\frac{A}{B}\)
Các bạn ơi giúp mk nhé !
sory baby bai nay dai cap minh o duoi nha xuong day lau lam nen ko lam nua sory baby lan nua
Đúng 0
Bình luận (0)
Em tham khảo tại link dưới đây nhé.
Câu hỏi của Nguyễn Lê Hoàng - Toán lớp 5 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Cho hình thang ABCD
a. Chỉ ra 1 hình chữ nhật (H) đồng phân với hình thang ABCD (có chứng minh)
b. Với hình chữ nhật(H) đã tìm được ở câu a và cho biết diện tích hình thang ABCD được tính như sau:
\(\frac{\left(a+c\right).b}{2}\). Hãy tìm diện tích hình chữ nhật(H)
14 tháng 6 2019 lúc 10:12
Cho hình bình hành ABCD , \(BD\perp BC\), biết AB = a , \(\widehat{A}=\alpha\). Tính diện tích hình bình hành đó .
Ai đúng và nhanh 3 tick nha !!! ( hình học nên mọi người giải nhớ vễ hình cho mk nha )Bài 1 : Tứ giác ABCD là hình gì, biết widehat{A}70^o;widehat{B}widehat{C}110^oBài 2 : Cho hình thang ABCD left(AB//CDright) . AC cắt BD tại O. Biết OA OB. Chứng minh rằng : ABCD là hình thang cân
Đọc tiếp
Ai đúng và nhanh 3 tick nha !!! ( hình học nên mọi người giải nhớ vễ hình cho mk nha )
Bài 1 : Tứ giác ABCD là hình gì, biết \(\widehat{A}=70^o;\widehat{B}=\widehat{C}=110^o\)
Bài 2 : Cho hình thang ABCD \(\left(AB//CD\right)\) . AC cắt BD tại O. Biết OA = OB. Chứng minh rằng : ABCD là hình thang cân
Bài 1: Nhường chủ tus và các bạn:D
Bài 2(ko chắc nhưng vẫn làm:v):
Do OA = OB(*) nên \(\Delta\)OAB cân tại O nên ^OAB = ^OBA (1)
Mặt khác cho AB // CD nên^OAB = ^OCD; ^OBA = ^ODC (so le trong) (2)
Từ (1) và (2) có ^OCD = ^ODC nên \(\Delta\) ODC cân tại O nên OC = OD (**)
Cộng theo vế (*) và (**) thu được:OA + OC = OB + OD
Hay AC = BD. Do đó hình thang ABCD có 2 đường chéo bằng nhau nên nó là hình thang cân (đpcm)
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh là a (m), a là số nguyên lớn hơn 1. Từ 1 điểm I nằm giữa B và D, kẻ IM vuông góc AB tại M.a) Trong trường hợp diện tích tam giác ICM frac{8}{9}m2, tính độ dài IM.b) Biết điểm M chia cạnh AB thành 2 phần sao cho frac{BM}{AB} frac{1}{a-1}và CM frac{4}{3}sqrt{10}(m). Tính độ dài cạnh hình vuông.
Đọc tiếp
Cho hình vuông ABCD có cạnh là a (m), a là số nguyên lớn hơn 1. Từ 1 điểm I nằm giữa B và D, kẻ IM vuông góc AB tại M.
a) Trong trường hợp diện tích tam giác ICM = \(\frac{8}{9}\)m2, tính độ dài IM.
b) Biết điểm M chia cạnh AB thành 2 phần sao cho \(\frac{BM}{AB}\)= \(\frac{1}{a-1}\)và CM = \(\frac{4}{3}\sqrt{10}\)(m). Tính độ dài cạnh hình vuông.
Cho hình thang ABCD có AB bằng \(\frac{1}{3}\)đáy CD . Kéo dài DA về phía A và CD phía B cắt nhau tại O . Biết S.AOB = 5 cm2 . tính S hình thang ABCD .
a) Hãy vẽ một tứ giác có hai đường chéo vuông góc với nhau, biết độ dài hai đường chéo đó là a và dfrac{1}{2}a. Hỏi có thể vẽ được bao nhiêu hình như vậy ?
b) Có thể vẽ được mấy hình thoi, biết độ dài hai đường chéo là a và dfrac{1}{2}a?
c) Hãy tính diện tích các hình vừa vẽ ?
Đọc tiếp
a) Hãy vẽ một tứ giác có hai đường chéo vuông góc với nhau, biết độ dài hai đường chéo đó là \(a\) và \(\dfrac{1}{2}a\). Hỏi có thể vẽ được bao nhiêu hình như vậy ?
b) Có thể vẽ được mấy hình thoi, biết độ dài hai đường chéo là \(a\) và \(\dfrac{1}{2}a\)?
c) Hãy tính diện tích các hình vừa vẽ ?
Cho hai điểm P , Q và 1 đường thẳng A không chứa P , Q ( hãy vẽ hình) Nêu cách tìm 1 điểm M trên đường thẳng a sao cho 3 điểm M , P , Q thẳng hàng. Hãy xét các trường hợp sau và cho biết trong trường hợp nào thì tìm được M nhyw thế :
- đường thẳng PQ cắt đường thẳng a
- đường thẳng PQ không cắt đường thẳng a( PQ song song với a)
Cho hình thang ABCD có góc A = góc B = 90 độ, AB = AD = \(\frac{1}{2}\)BC. Biết CD = \(\sqrt{50}\)cm. Tính độ dài cạnh BC