tìm d' là ảnh của d với
a) \(d:x-3y+5=0\); \(\alpha=60^o\)
b) \(d:2x-y+6=0\); \(\alpha=45^o\)
Những câu hỏi liên quan
23 tháng 4 2023 lúc 10:34
1. Phương trình tiếp tuyến d của đường tròn (C): x^2+y^2-3x-y0 tại điểm N(1;-1) là:A. d:x+3y-20 B. d:x-3y+40 C. d:x-3y-40 D. d:x+3y+20 2. Cho đường tròn (C): x^2+y^2-4x+4y-40 và điểm M(1;0). Dây cung của (C) đi qua điểm M có độ dài ngắn nhất bằng:A. 2sqrt{3} B. sqrt{5} C. 12 D. 2sqrt{7}3. Lập phương trình chính tắc của parabol (P) biết (P) đi qua điểm M có hoành độ x_M2 và kh...
Đọc tiếp
1. Phương trình tiếp tuyến d của đường tròn (C): \(x^2+y^2-3x-y=0\) tại điểm N(1;-1) là:
A. \(d:x+3y-2=0\) B. \(d:x-3y+4=0\)
C. \(d:x-3y-4=0\) D. \(d:x+3y+2=0\)
2. Cho đường tròn (C): \(x^2+y^2-4x+4y-4=0\) và điểm M(1;0). Dây cung của (C) đi qua điểm M có độ dài ngắn nhất bằng:
A. \(2\sqrt{3}\) B. \(\sqrt{5}\) C. 12 D. \(2\sqrt{7}\)
3. Lập phương trình chính tắc của parabol (P) biết (P) đi qua điểm M có hoành độ \(x_M=2\) và khoảng từ M đến tiêu điểm là \(\dfrac{5}{2}\)
A. \(y^2=8x\) B. \(y^2=4x\) C. \(y^2=x\) D. \(y^2=2x\)
21 tháng 9 2020 lúc 22:25
cho \(d:x-3y+5=0\)
Tìm d' là ảnh của d qua phép quay \(Q\left(0;60^o\right)\)
Nguyễn Việt Lâm: Giup mk vs bn.. :]]
Ai giải giúp e vs ạ, em cảm ơn nhiều
1)cho d:x-3y+2=0 viết pt đường thẳng d' là ảnh của đ qua phép Tv, Q(o,90 độ) V(o,2)
2)cho đường tròn C) : x^2 -y^2 =5. Tìm ảnh của (C) qua phép đồng dạng đc thực hiện liên tiếp bởi phép V(o;-2) Q(o,90 độ)
Trong mặt phẳng
v
→
(
−
2
;
1
)
cho, đường thẳng d có phương trình 2x − 3y + 3 0, đường thẳng
d
1
có phương trình
2
x
−
3
y
−
5
0
.
Tìm t...
Đọc tiếp
Trong mặt phẳng v → = ( − 2 ; 1 ) cho, đường thẳng d có phương trình 2x − 3y + 3 = 0, đường thẳng d 1 có phương trình 2 x − 3 y − 5 = 0 .
Tìm tọa độ của w → có giá vuông góc với đường thẳng d để d 1 là ảnh của d qua T w →
Lấy một điểm thuộc d, chẳng hạn M = (0; 1).
Đường thẳng d 2 qua M vuông góc với có vectơ chỉ phương là v → = ( 2 ; − 3 ) .
Do đó phương trình của
d
2
là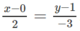 
.
Gọi M' là giao của d 1 với d 2 thì tọa độ của nó phải thỏa mãn hệ phương trình:
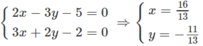
Từ đó suy ra
Đúng 0
Bình luận (0)
Cho đường thẳng (d): x – 3y 0, đường thẳng (d’): x – 3y – 10 0. Tìm tọa độ vectơ
u
→
có giá vuông góc với đường thằng (d) để (d’) là ảnh của (d) qua
T
u
→
A.
1
;
−
3
B.
2
;
−
6
C.
3...
Đọc tiếp
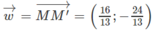
Cho đường thẳng (d): x – 3y = 0, đường thẳng (d’): x – 3y – 10 = 0. Tìm tọa độ vectơ u → có giá vuông góc với đường thằng (d) để (d’) là ảnh của (d) qua T u →
A. 1 ; − 3
B. 2 ; − 6
C. 3 ; − 9
D. Một kết quả khác
Đáp án A
Vectơ pháp tuyến của đường thẳng d là v → (1; –3). Ta có u → = k v → ( k ≠ 0 do d ≠ d ' )
⇔ u → ( k ; − 3 k ) . Áp dụng biểu thức tọa độ, ta có: x ' = k + x y ' = − 3 k + y ( trong đó x’; y’ thỏa mãn phương trình đường thẳng (d’))
=> k + x – 3( –3k + y) – 10 = 0 => x − 3 y + 10 k – 10 = 0 x − 3 y = 0 => k = 1
Đúng 0
Bình luận (0)
Viết phương trình đường thẳng d đi qua A(-2 ; 0) và tạo với đường thẳng d:x+3y–3 0 một góc 450. A. x+ y-3 0 và x- 2y + 2 0 B. 2x+ y+ 4 0 và x-2y +2 0 C. x+ 2y-3 0 và 2x-y+4 0 D. x-2y+1 0 và 2x+ y- 6 0
Đọc tiếp
Viết phương trình đường thẳng d đi qua A(-2 ; 0) và tạo với đường thẳng d:x+3y–3= 0 một góc 450.
A. x+ y-3= 0 và x- 2y + 2= 0
B. 2x+ y+ 4= 0 và x-2y +2= 0
C. x+ 2y-3= 0 và 2x-y+4= 0
D. x-2y+1 = 0 và 2x+ y- 6= 0
Đáp án B
Phương trình đường thẳng d đi qua A ( -2; 0) có dạng: A(x+ 2) + By= 0.
Theo giả thiết, ta có:
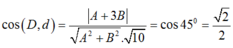
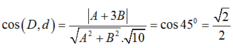
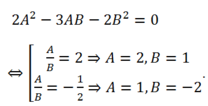
Vậy: d: 2x+ y+ 4= 0 hoặc d: x- 2y + 2= 0.
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho (-7;2)và đường thẳng d:x-2y+10=0 Tìm phương trình đường thẳng d' là ảnh của d qua phép vị tự tâm I tỉ số vị tự bằng 3.
Lấy A(2;6) thuộc d
Theo đề, ta có; \(\overrightarrow{IA'}=3\cdot\overrightarrow{IA}\)
=>\(\left\{{}\begin{matrix}x+7=3\left(2+7\right)\\y-2=3\left(6-2\right)\end{matrix}\right.\Leftrightarrow A'\left(20;14\right)\)
Thay x=20 và y=14 vào (d'): x-2y+c=0, ta đc:
c+20-28=0
=>c=8
Đúng 0
Bình luận (0)
Trong mặt phẳng (Oxy), cho \(d:x+y-2=0\)
Viết phương trình của đường thẳng d' là ảnh của d qua phép \(Q_{\left(0;45^0\right)}\)
Trong không gian Oxyz, cho đường thẳng
d
:
x
-
2
3
y
+
1
1
z
+
5
-
1
và mặt phẳng (P):2x-3y+z-60. Phương trình nào...
Đọc tiếp
Trong không gian Oxyz, cho đường thẳng d : x - 2 3 = y + 1 1 = z + 5 - 1 và mặt phẳng (P):2x-3y+z-6=0. Phương trình nào dưới đây là phương trình của đường thẳng nằm trong mặt phẳng (P), cắt và vuông góc với (d)?
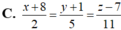
Chọn A
Phương trình tham số của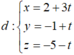 
Ta có M = d ∩ (P) nên 2 (2+3t)-3 (-1+t)-5-t-6=0 ó t = 2 => M (8 ; 1 ; -7)
VTCP của Δ là 
Δ đi qua M có VTCP 
nên có phương trình: 
Đúng 0
Bình luận (0)