Cho Parabol (P) và đường thẳng (d) có phương trình:
(P): y = x2/2 ; (d): y= mx - m+2
Tìm m để đường thẳng (d) và (P) cùng đi qua một điển có hoành độ = 4Giúp mình nhé
a.Cho parabol (P): y = x2 và đường thẳng (d): y = 3x - 2
Hãy tìm tọa độ giao điểm của đường thẳng (d) và parabol(P) bằng phương pháp đại số.
b.Cho phương trình x2 - 2(m + 1)x + 2m - 3 = 0
với m là tham số.Chứng minh rằng phương trình luôn có hai nghiệm phân biệt với mọi giá trị của m.
a: PTHĐGĐ là:
x^2-3x+2=0
=>(x-2)(x-1)=0
=>x=2 hoặc x=1
Khi x=2 thì y=2^2=4
Khi x=1 thì y=1^2=1
b: Δ=(2m+2)^2-4(2m-3)
=4m^2+8m+4-8m+12
=4m^2+16>0
=>Phương trình luôn có hai nghiệm
Cho parabol (P): y = \(\dfrac{1}{2}\)x2 và đường thẳng (d): y = 3x - 4
Viết phương trình đường thẳng (d1): y = ax + b song song với (d) và cắt (P) tại điểm A có hoành độ bằng -2
Vì (d1)//(d) nên \(\left\{{}\begin{matrix}a=3\\b\ne-4\end{matrix}\right.\)
Vậy: (d1): y=3x+b
Thay x=-2 vào (P), ta được:
\(y=\dfrac{1}{2}\cdot\left(-2\right)^2=\dfrac{1}{2}\cdot4=2\)
Thay x=-2 và y=2 vào (d1), ta được:
\(3\cdot\left(-2\right)+b=2\)
\(\Leftrightarrow b=8\)(thỏa ĐK)
Vậy: (d1): y=3x+8
để \(\left(d1\right)\) sogn song với \(\left(d\right)\)
\(< =>\left\{{}\begin{matrix}a=3\\b\ne-4\end{matrix}\right.\)
để (d1) cắt (P) tại A có hoành độ -2\(=>x=-2\)
\(=>\dfrac{1}{2}x^2=3x+b< =>\dfrac{1}{2}\left(-2\right)^2=3\left(-2\right)+b=>b=8\left(tm\right)\)
=>\(\left(d1\right):y=3x+8\)
a) Tìm các giá trị tham số m để phương trình x2 – (2m – 3)x + m(m – 3) = 0 có 2 nghiêm phân biệt x1; x2 thỏa mãn điều kiện 2x1 – x2 = 4
b) Cho Parabol (P): \(y=-3x^2\) và đường thẳng (d): \(y=2x-m+9\) .Tìm m để đường thẳng (d) cắt Parabol (P) tại hai điểm nằm về hai phía của trục tung.
trong mặt phẳng tọa độ Oxy. Cho parabol (P) có phương trình y=x2 và đường thẳng (d) có phương trình y=5x -m + 2 ( m là tham số )
1) Điểm A=(2;4) có thuộc đô thị hàm số (P) không. Tại sao
2) Tìm m để dường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có tung độ y1,y2 tỏa mãn y1 + y2 + y1 x y2
1: f(2)=2^2=4
=>A thuộc (P)
2: bạn bổ sung lại đề đi bạn
Cho parabol (P) có phương trình y = x 2 và đường thẳng d đi qua A(1;3). Giả sử khi đường thẳng d có hệ số góc k thì diện tích hình phẳng giới hạn bởi parabol (P) và đường thẳng d là nhỏ nhất. Giá trị thực của k thuộc khoảng nào sau đây?
A. 3 ; + ∞
B. − ∞ ; − 3
C. (0;3)
D. (-3;0)
Phương pháp:
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số
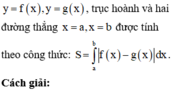
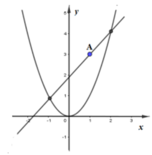

Diện tích hình phẳng giới hạn bởi parabol (P) và đường thẳng d:
S = ∫ x 1 x 2 k x − k + 3 − x 2 d x = 1 2 k x 2 − k − 3 x − 1 3 x 3 x 2 x 1 = 1 2 k x 1 2 − k − 3 x 1 − 1 3 x 1 3 − 1 2 k x 2 2 − k − 3 x 2 − 1 3 x 2 3 = 1 2 k x 1 2 − x 2 2 − k − 3 x 1 − x 2 − 1 3 x 1 3 − x 2 3 = x 1 − x 2 1 2 k x 1 + x 2 − k − 3 − 1 3 x 1 + x 2 2 − x 1 x 2 = x 1 − x 2 1 2 k . k − k − 3 − 1 3 k 2 − k − 3 = x 1 − x 2 1 6 k 2 − 2 3 k + 2
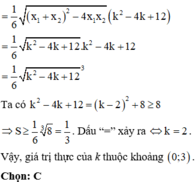
1. Giải phương trình x (x - 1) (x2 - x + 1) = 6.
2. Trong mặt phẳng tọa độ Oxy, cho parabol (P): y=x2 và đường thẳng d: y = 2x - m +1
Gọi E và F là 2 diểm thuộc (P) có hoành độ lần lượt là -1 và 3. Xác định tọa độ E và F và viết phương trình đường thẳng đi qua 2 điểm E và F.
Cho phương trình d: y = (m + 1)x - m ( m là tham số) và Parabol (P): y = 1/2 x2
1) Tìm m để đường thẳng d cắt trục hoành tại điểm có hoành độ bằng 2.
2) Tìm m để đường thẳng d cắt (P) tại 2 điểm phân biệt có hoành độ x1, x2 thỏa mãn căn x1 + căn x2 = căn 2
Câu 1 : Cho hàm số y = 1/2x² có đồ thị là parabol và đường thẳng d có phương trình là y = x + m. Tìm m để d cắt parabol tại hai điểm phân biệt A( x1; y1) B(x2 ; y2) và thỏa mãn 1/2y1 + 1/2y2 = 2
Câu 2: cho một tam giác có đường cao với độ dài bằng một nửa độ dài cạnh đáy tương ứng nếu tăng chiều cao thêm 2 m và cạnh tương ứng tăng thêm 6 m thì được một tam giác có diện tích gấp đôi diện tích tam giác ban đầu Tính diện tích của tam giác ban đầu
Đường thẳng d: y = mx + n và parabol (P): y = a. x 2 (a ≠ 0) không cắt nhau phương trình a x 2 = m.x + n
A. Hai nghiệm phân biệt
B. Nghiệm kép
C. Vô nghiệm
D. Có hai nghiệm âm
Đường thẳng d và parabol (P) tiếp xúc với nhau khi phương trình a. x 2 = m.x + n ↔a. x 2 − m.x – n = 0 vô nghiệm (∆< 0)
Đáp án: C
1.cho parabol (P): y=x2 và đường thẳng (d) y=x+m-1. Tìm m sao cho d cắt (P) tại 2 điểm phân biệt nằm ở bên phải trục tung
2.Lập phương trình bậc hai có 2 nghiệm 2-căn 3 và 2+căn 3
1: PTHĐGĐ là:
x^2-x-m+1=0(1)
Δ=(-1)^2-4(-m+1)=1+4m-4=4m-3
Để (P) cắt (d) tại hai điểm phân biệt thì 4m-3>0
=>m>3/4
Để (1) có hai nghiệm dương phân biệt thì m>3/4 và 1>0 và -m+1>0
=>m>3/4 và -m>-1
=>3/4<m<1