Cho \(\Delta MNP\) có \(\widehat{M}=30^o;\widehat{N}=20^o\) trên MN lấy D sao cho MD= NP. Tính \(\widehat{NPD}\)

Những câu hỏi liên quan
Cho \(\Delta MNP\)có \(\widehat{M}=30^o\); \(\widehat{N}=30^o\). Trên cạnh MN lấy D sao cho MD=NP. Tính \(\widehat{NPD}\)
Cho \(\Delta MNP\) có \(\widehat{M}=30^o;\widehat{N}=20^o\) trên MN lấy D sao cho MD= NP. Tính \(\widehat{NPD}\)
em mới lớp 6 nhung đoạc thấy nó cứ giống toán 6 nâng cao
nhưng ko bt có đúng ko *-* ^-^
Đúng 0
Bình luận (0)
Cho \(\Delta MNP\)có \(\widehat{M}=30^o\); \(\widehat{N}=20^o\). Trên cạnh MN lấy D sao cho MD= NP. Tính \(\widehat{NPD}\)
Cho \(\Delta MNP\) có \(\widehat{M}=30^o\); \(\widehat{N}=20^o\) . Trên MN lấy D sao cho MD=NP. Tính \(\widehat{NPD}\)
Cho \(\Delta MNP\)có \(\widehat{M}=30^o\); \(\widehat{N}=20^o\). Trên cạnh MN lấy D sao cho MD= NP. Tính \(\widehat{NPD}\)
Cho \(\Delta MNP\)có \(\widehat{M}=30^o\); \(\widehat{N}=20^o\). Trên cạnh MN lấy D sao cho MD= NP. Tính \(\widehat{NPD}\).
Cho \(\Delta MNP\)có \(\widehat{M}=30^o\); \(\widehat{N}=30^o\). Trên cạnh MN lấy D sao cho MD=NP. Tính \(\widehat{NPD}\)
Cho tam giác MNP có \(\widehat M = \widehat N\). Vẽ tia phân giác PK của tam giác \(MNP(K \in MN)\).
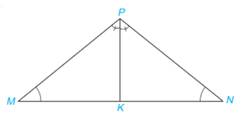
Chứng minh rằng:
a) \(\widehat {MKP} = \widehat {NKP}\);
b) \(\Delta MPK = \Delta NPK\);
c) Tam giác MNP có cân tại \(P\) không?
a)
Xét tam giác MPK có:
\(\widehat {PKM} + \widehat {MPK} + \widehat {KMP} = {180^o}\)
Xét tam giác NPK có:
\(\widehat {PKN} + \widehat {NPK} + \widehat {KNP} = {180^o}\)
Mà \(\widehat {KMP} = \widehat {KNP};\,\,\,\widehat {MPK} = \widehat {NPK}\)
Suy ra \(\widehat {MKP} = \widehat {NKP}\).
b)Xét hai tam giác MPK và NPK có:
\(\widehat {MPK} = \widehat {NPK}\)
PK chung
\(\widehat {MKP} = \widehat {NKP}\)
=>\(\Delta MPK = \Delta NPK\)(g.c.g)
c) Do \(\Delta MPK = \Delta NPK\) nên MP=NP (2 cạnh tương ứng)
=> Tam giác MNP cân tại P.
Đúng 0
Bình luận (0)
Cho \(\Delta MNP\) có \(\widehat{M}=30^o\); \(\widehat{N}=20^o\) . Trên MN lấy D sao cho MD=NP. Tính \(\widehat{NPD}\)
cho hỏi là cái kia là MN kéo dài hay là D∈MN
Đúng 0
Bình luận (1)









