Tọa độ giao điểm của (d1) và (d3) là:

\(\left\{{}\begin{matrix}2x-1=-x+3\\y=-x+3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3x=4\\y=-x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{4}{3}\\y=-\dfrac{4}{3}+3=\dfrac{5}{3}\end{matrix}\right.\)

Thay x=4/3 và y=5/3 vào (d2), ta được:

\(\dfrac{4}{3}\left(2n-1\right)+\dfrac{3}{2}=\dfrac{5}{3}\)

=>\(\dfrac{8}{3}n-\dfrac{4}{3}+\dfrac{3}{2}=\dfrac{5}{3}\)

=>\(\dfrac{8}{3}n=\dfrac{5}{3}+\dfrac{4}{3}-\dfrac{3}{2}=\dfrac{3}{2}\)

=>\(n=\dfrac{3}{2}:\dfrac{8}{3}=\dfrac{3}{2}\cdot\dfrac{3}{8}=\dfrac{9}{16}\)

a: d//d1

=>m-2=-m và m+7<>2m-3

=>m=1

b: d trùng với d2

=>m-2=-m^2 và m+7=-2m+1

=>m=-2 và m^2+m-2=0

=>m=-2

d: d vuông góc d4

=>-1/6(m+3)(m-2)=-1

=>(m+3)(m-2)=6

=>m^2+m-6-6=0

=>m^2+m-12=0

=>m=-4 hoặc m=3

c: Thay y=1/3 vào d3, ta được:

-2/3x+5/3=1/3

=>-2/3x=-4/3

=>x=2

Thay x=2 và y=1/3 vào (d), ta được:

2(m-2)+m+7=1/3

=>3m+3=1/3

=>3m=-8/3

=>m=-8/9

1) Ta có: \(\left\{{}\begin{matrix}2\cdot\dfrac{x}{x+2}-\dfrac{y}{y-1}=4\\\dfrac{x}{x+2}-3\cdot\dfrac{y}{y-1}=-3\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2\cdot\dfrac{x}{x+2}-\dfrac{y}{y-1}=4\\2\cdot\dfrac{x}{x+2}-6\cdot\dfrac{y}{y-1}=-6\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}-7\cdot\dfrac{y}{y-1}=10\\2\cdot\dfrac{x}{x+2}-\dfrac{y}{y-1}=4\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{y}{y-1}=\dfrac{-10}{7}\\2\cdot\dfrac{x}{x+2}+\dfrac{10}{7}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2\cdot\dfrac{x}{x+2}=\dfrac{18}{7}\\\dfrac{y}{y-1}=\dfrac{-10}{7}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{x+2}=\dfrac{9}{7}\\\dfrac{y}{y-1}=\dfrac{-10}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9\left(x+2\right)=7x\\-10\left(y-1\right)=7y\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}9x+18-7x=0\\-10y+10-7y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+18=0\\-17y+10=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x=-18\\-17y=-10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-9\\y=\dfrac{10}{17}\end{matrix}\right.\)

Vậy: Hệ phương trình có nghiệm duy nhất là \(\left(x,y\right)=\left(-9;\dfrac{10}{17}\right)\)

4 phần tử?

[-3;-1/3)U(1/3;3]?

Với m = 1 

(d₁) có dạng y = x + 3

(d₂) có dạng y = -x + 3

Phương trình hoành độ giao điểm 

-x + 3 = x + 3

<=> x = 0

Với x = 0 <=> y = 3

Tọa độ giao điểm A(0;3) 

Bây giờ ta sẽ đi tìm tọa độ giao điểm của 3 đường thẳng trên

Với (d₁) và (d₂) cắt nhau tại điểm \(A\left(x_1;y_1\right)\) nên khi đó:
\(\hept{\begin{cases}y_1=3x_1-2\\y_1=-\frac{1}{3}x_1+\frac{4}{3}\end{cases}}\Rightarrow3x_1-2=-\frac{1}{3}x_1+\frac{4}{3}\Leftrightarrow\frac{10}{3}x_1=\frac{10}{3}\Rightarrow\hept{\begin{cases}x_1=1\\y_1=1\end{cases}}\)

Vậy \(A\left(1;1\right)\)

Tương tự gọi B,C là giao điểm của đường (d₃) với (d₂) , (d₁) 

Khi đó ta dễ dàng tính được: \(B\left(4;0\right)\) ; \(C\left(2;4\right)\)

Áp dụng công thức tính khoảng cách giữa 2 điểm trong mặt phẳng ta có:
\(AB=\sqrt{\left(1-4\right)^2+\left(1-0\right)^2}=\sqrt{10}\Rightarrow AB^2=10\)

\(AC=\sqrt{\left(1-2\right)^2+\left(1-4\right)^2}=\sqrt{10}\Rightarrow AC^2=10\)

\(BC=\sqrt{\left(4-2\right)^2+\left(0-4\right)^2}=\sqrt{20}\Rightarrow BC^2=20\)

Xét tam giác ABC có: \(\hept{\begin{cases}AB=AC\\AB^2+AC^2=BC^2\left(=20\right)\end{cases}}\)

=> Tam giác ABC vuông cân tại A

=> đpcm

giao điểm của d1 với d2 là : y=3x-2

                                              y=-1/3x+4/3

                                           <=> 3x -2 =-1/3+4/3

                                                    y=3x-2

                                               <=> x=1

                                                       y=1

vaaky giao điểm của d1 và d2 có tọa độ A(1,1)

tương tự ta được giao điểm của: d2 với d3 có tọa độ B (4,0)

                                                       d3 với d1 có tọa độ C(2,4)

độ dài AB là\(\sqrt{\left(Xa-Xb\right)^2+\left(Ya+Yb\right)^2}\)=\(\sqrt{\left(1-4\right)^2+\left(1-0\right)^2}\)=\(\sqrt{10}\)

tương tư ta được AC= \(\sqrt{10}\)

=> AB=AC ; d1 vuông góc d2 vì 3.(-1/3)=-1

=> tam giác ABC VUÔNG CÂN

Ta có:d1=d2                                         <=>3x-2=-1

1: Khi m=1 thì (d1): y=x+3 và (d2): y=-x+3

a: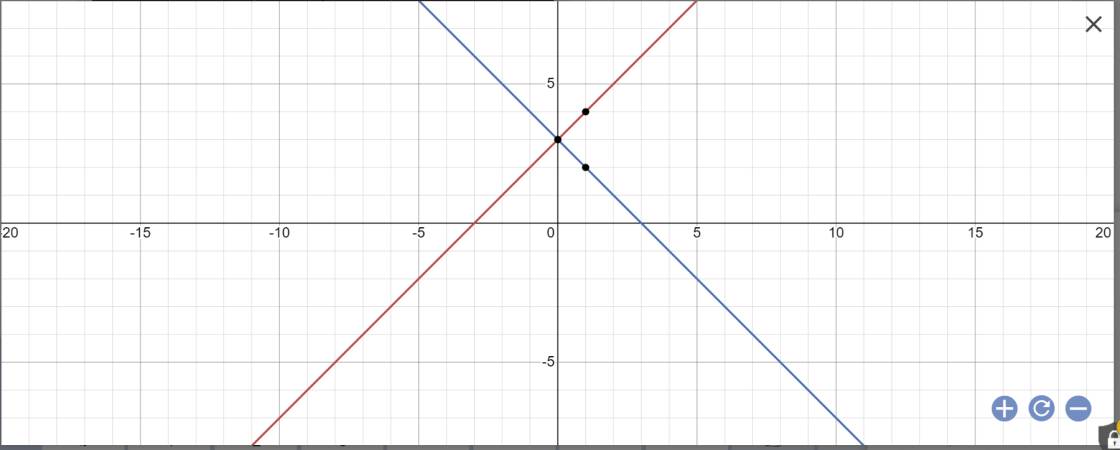 

b: Tọa độ giao điểm là:

x+3=-x+3 và y=x+3

=>x=0 và y=3

Tọa độ giao điểm của (d2) và (d3) là nghiệm của hệ phương trình sau:

\(\left\{{}\begin{matrix}x+1=-x+3\\y=x+1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x=2\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)

Thay x=1 và y=2 vào (d1), ta được:

\(\left(m^2-1\right)+m^2-5=2\)

=>\(2m^2=8\)

=>\(m^2=4\)

=>\(\left[{}\begin{matrix}m=2\\m=-2\end{matrix}\right.\)