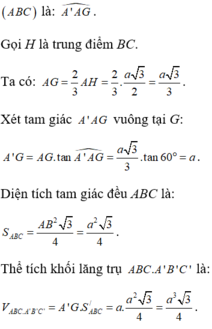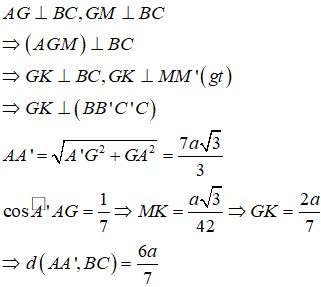cho lăng trụ abc a'b'c' đáy là tam giác đều cạnh đáy a. A' cách đều 3 điểm A,B,C. [AA'(ABC)]=60 chứng minh B'C'CB là hình chữ nhật . tính Sxq

Những câu hỏi liên quan
Cho khối lăng trụ ABC ABC có đáy là tam giác đều cạnh a, điểm A cách đều ba điểm A, B, C. Cạnh bên AA tạo với mặt phẳng đáy một góc 60°. Thể tích khối lăng trụ ABC ABC là A.
a
3
3
B.
a
3
3
2
C.
a
3
3...
Đọc tiếp
Cho khối lăng trụ ABC A'B'C' có đáy là tam giác đều cạnh a, điểm A' cách đều ba điểm A, B, C. Cạnh bên AA' tạo với mặt phẳng đáy một góc 60°. Thể tích khối lăng trụ ABC A'B'C' là
A. a 3 3
B. a 3 3 2
C. a 3 3 6
D. a 3 3 4
Cho hình lăng trụ ABC. ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Biết khoảng cách giữa hai đường thẳng AA và BC bằng
a
3
4
. Tính theo a thể tích V của khối lăng trụ ABC. ABC. A.
a
3
3
6
B. ...
Đọc tiếp
Cho hình lăng trụ ABC. A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A' lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Biết khoảng cách giữa hai đường thẳng AA' và BC bằng a 3 4 . Tính theo a thể tích V của khối lăng trụ ABC. A'B'C'.
A. a 3 3 6
B. a 3 3 12
C. a 3 3 3
D. a 3 3 24
Chọn B
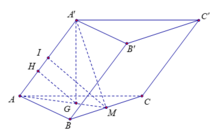
Ta có A ' G ⊥ A B C nên A ' G ⊥ B C ; B C ⊥ A M ⇒ B C ⊥ M A A '
Kẻ M I ⊥ A A ' ; B C ⊥ I M nên d A A ' ; B C = I M = a 3 4
Kẻ G H ⊥ A A ' , ta có
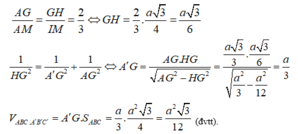
Đúng 0
Bình luận (0)
Cho lăng trụ ABC ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A’ lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Biết thể tích của khối lăng trụ là
a
3
3
4
. Tính khoảng cách giữa hai đường thẳng AA và BC. A.
4
a
3
B.
2
a...
Đọc tiếp
Cho lăng trụ ABC A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A’ lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Biết thể tích của khối lăng trụ là a 3 3 4 . Tính khoảng cách giữa hai đường thẳng AA' và BC.
A. 4 a 3
B. 2 a 3
C. 3 a 4
D. 3 a 2
Đáp án D
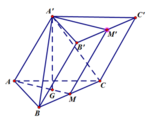
Ta có d ( AA ' , B C ) = d ( A A ' , ( B B ' C ' C ) ) = d ( A ' , ( B B ' C ' C ) )
Gọi M và M’ lần lượt là trung điểm BC và B’C’, G là trọng tâm của tam giác ABC
Theo giả thiết ta có B C ⊥ A M B C ⊥ A ' G ⇒ B C ⊥ ( A A ' G ) ⇒ B C ⊥ A A ' , nên tứ giác BB’C’C là hình chữ nhật có cạnh BC = a
Vì
V A ' A B C = 1 3 A ' G . S Δ A B C = 1 3 V L T = a 3 3 12 ⇒ A ' G = a ⇒ A A ' = A G 2 + A ' G 2 = 2 a 3
Có
V A ' B B ' C ' C = 2 3 V L T = a 3 3 6 = 1 3 d ( A ' , ( B B ' C ' C ) ) . S B B ' C ' C ⇒ d ( A ' , ( B B ' C ' C ) ) = 3 a 2
Đúng 0
Bình luận (0)
Cho lăng trụ ABC ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A’ lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Biết thể tích của khối lăng trụ là
a
3
3
4
. Tính khoảng cách giữa hai đường thẳng AA và BC. A.
4
a
3
B.
2
a...
Đọc tiếp
Cho lăng trụ ABC A'B'C có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A’ lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Biết thể tích của khối lăng trụ là a 3 3 4 . Tính khoảng cách giữa hai đường thẳng AA' và BC.
A. 4 a 3
B. 2 a 3
C. 3 a 4
D. 3 a 2
Đáp án D
Ta có d ( AA ' , B C ) = d ( A A ' , ( B B ' C ' C ) ) = d ( A ' , ( B B ' C ' C ) )
Gọi M và M’ lần lượt là trung điểm BC và B’C’, G là trọng tâm của tam giác ABC
Theo giả thiết ta có B C ⊥ A M B C ⊥ A ' G ⇒ B C ⊥ ( A A ' G ) ⇒ B C ⊥ A A ' , nên tứ giác BB’C’C là hình chữ nhật có cạnh BC = a
Vì
V A ' A B C = 1 3 A ' G . S Δ A B C = 1 3 V L T = a 3 3 12 ⇒ A ' G = a ⇒ A A ' = A G 2 + A ' G 2 = 2 a 3
⇒ S B B ' C ' C = 2 a 2 3
Có V A ' B B ' C ' C = 2 3 V L T = a 3 3 6 = 1 3 d ( A ' , ( B B ' C ' C ) ) . S B B ' C ' C ⇒ d ( A ' , ( B B ' C ' C ) ) = 3 a 2
Chọn D
Đúng 0
Bình luận (0)
Cho hình lăng trụ ABC. ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A’ lên (ABC) trùng với tâm O của tam giác ABC, thể tích của khối lăng trụ ABC. ABC bằng
3
a
3
. Tính khoảng cách h giữa hai đường thẳng AA và BC A.
h
a
B.
h
7
a
6
C.
h
6...
Đọc tiếp
Cho hình lăng trụ ABC. A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A’ lên (ABC) trùng với tâm O của tam giác ABC, thể tích của khối lăng trụ ABC. A'B'C' bằng 3 a 3 . Tính khoảng cách h giữa hai đường thẳng AA' và BC
A. h = a
B. h = 7 a 6
C. h = 6 a 7
D. h = a 3 2
Cho hinh lăng trụ A'B'C' có đáy ABC là tam giác đều cạnh a, hình chiếu của A' trên (ABC) là trung điểm đoạn thẳng AB. Biết AA’ = 2a. Thể tích của khối lăng trụ A'B'C'ABC là
Do \(AA'\text{/ / }CC'\Rightarrow AA'\) tạo với (ABC) một góc \(45^o\)
Mà \(A'H\text{⊥}\left(ABC\right)\Rightarrow\widehat{A'AH}\) là góc giữa \(AA'\) và ( ABC)
\(\Rightarrow\widehat{A'AH=45^o\Rightarrow}\Delta A'AH\) vuông cân tại H
\(\Rightarrow A'H=AH=\dfrac{AB}{2}=\dfrac{a}{2}\)
\(^SABC=\dfrac{a^2\sqrt{3}}{4}=V=^SABC.^{A'H}=\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^3.\sqrt{3}}{8}\)
Đúng 2
Bình luận (0)
Cho hình lăng trụ ABC ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC. Biết thể tích của khối lăng trụ là
a
3
3
4
. Tính khoảng cách giữa hai đường thẳng AA và BC A.
4
a
3
B.
2
a
3...
Đọc tiếp
Cho hình lăng trụ ABC A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A' lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC. Biết thể tích của khối lăng trụ là a 3 3 4 . Tính khoảng cách giữa hai đường thẳng AA' và BC
A. 4 a 3
B. 2 a 3
C. 3 a 4
D. 3 a 2
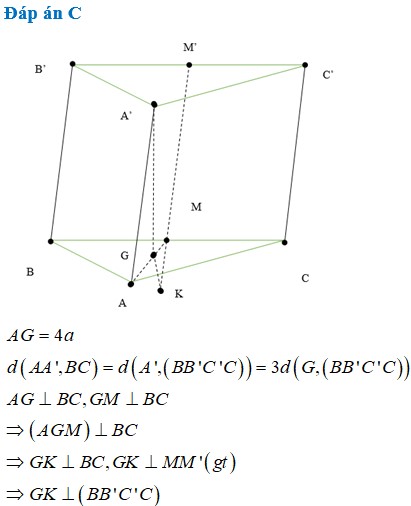
Đáp án C
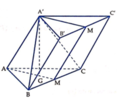
Ta dễ dàng chứng minh được A A ' / / B C C ' B '
⇒ d A A ' ; B C = d A A ' ; B C C ' B ' = d A ; B C C ' B '
Gọi G là trọng tâm của tam giác ABC. Suy ra A ' G ⊥ A B C .
Ta có S Δ A B C = a 2 3 4
⇒ V A B C . A ' B ' C ' = A ' G . S Δ A B C ⇔ A ' G = V A B C . A ' B ' C ' S Δ A B C = a 3 3 4 : a 2 3 4 = a
Lại có
A M = a 3 2 ⇒ A G = 2 3 A M = a 3 3 ⇒ A A ' = A ' G 2 + A G 2 = 2 a 3 3
Ta luôn có V A ' . A B C = 1 3 V A B C . A ' B ' C ' = 1 3 . a 3 3 4 = a 3 3 12 .
Mà V A B C . A ' B ' C ' = V A ' . A B C + V A ' . B C C ' B '
⇒ V A ' . B C C ' B ' = V A B C . A ' B ' C ' − V A ' . A B C = a 3 3 4 − a 3 3 12 = a 3 3 6 .
Gọi M,M' lần lượt là trung điểm của BC và B'C'. Ta có B C ⊥ A M , B C ⊥ A ' G ⇒ B C ⊥ A M M ' A ' ⇒ B C ⊥ M M ' . Mà M M ' / / B B ' nên B C ⊥ B B ' ⇒ B C C ' B ' là hình chữ nhật
⇒ S B C C ' B ' = B B ' . B C = 2 a 3 3 . a = 2 a 2 3 3 .
Từ
V A ' . B C C ' B ' = 1 3 d A ' ; B C C ' B ' . S B C C ' B ' ⇔ d A ' ; B C C ' B ' = 3 V A ' . B C C ' B ' S B C C ' B '
⇒ d A ' ; B C C ' B ' = a 3 3 2 : 2 a 2 3 3 = 3 a 4 . Vậy d A A ' ; B C = 3 a 4 .
Đúng 0
Bình luận (0)
Cho lăng trụ xiên tam giác ABC ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu của A xuống (ABC) là tâm O đường tròn ngoại tiếp tam giác ABC biết AA hợp với đáy ABC một góc
60
°
.
Tính thể tích lăng trụ A.
3
a
3
3
4
B.
a
3
3...
Đọc tiếp
Cho lăng trụ xiên tam giác ABC A'B'C' có đáy ABC là tam giác đều cạnh a. Hình chiếu của A' xuống (ABC) là tâm O đường tròn ngoại tiếp tam giác ABC biết AA' hợp với đáy ABC một góc 60 ° . Tính thể tích lăng trụ
A. 3 a 3 3 4
B. a 3 3 4
C. a 3 12
D. a 3 2
Đáp án B
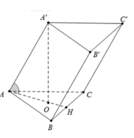
Ta có: S đ = a 2 3 4 ; O A = 2 3 A H = a 3 3
Mặt khác AA' hợp với đáy ABC một góc 60 ∘
nên A ' O H ⏜ = 60 ∘ suy ra A ' H = O A tan 60 ∘ = a .
Suy ra V A B C . A ' B ' C ' = S đ h = a 3 3 4
Đúng 0
Bình luận (0)
Cho khối lăng trụ ABC.ABC có đáy là tam giác đều cạnh a, điểm A cách đều ba điểm A, B, C. Cạnh bên AA tạo với mặt phẳng đáy một góc 60°. Thể tích khối lăng trụ ABC.ABC là: A.
a
3
3
B.
a
3
3
2
C.
a
3
3...
Đọc tiếp
Cho khối lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a, điểm A' cách đều ba điểm A, B, C. Cạnh bên AA' tạo với mặt phẳng đáy một góc 60°. Thể tích khối lăng trụ ABC.A'B'C' là:
A. a 3 3
B. a 3 3 2
C. a 3 3 6
D. a 3 3 4
Chọn đáp án D.
Ta có A'A = A'B = A'C nên hình chiếu của A' là tâm đường tròn ngoại tiếp tam giác ABC.
Do tam giác ABC đều nên trọng tâm G là tâm đường tròn ngoại tiếp tam giác ABC.
![]()
AG là hình chiếu của A'A lên mặt phẳng (ABC)
Góc giữa A'A với mặt phẳng (ABC) là: A ' A G ^
Gọi H là trung điểm BC.
Ta có: 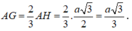
Xét tam giác A'AG vuông tại G:
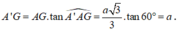
Diện tích tam giác đều ABC là:
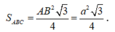
Thể tích khối lăng trụ ABC.A'B'C' là:
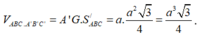
Đúng 0
Bình luận (0)