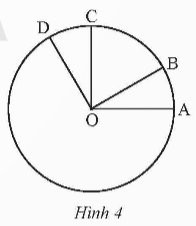
Quan sát Hình 4. Biết \(\widehat {DOA} = {120^o}\), OA \( \bot \)OC, OB \( \bot \)OD.
a) Đọc tên các góc ở tâm có trong hình.
b) Tính số đo của mỗi góc ở tâm tìm được ở câu a
c) Tìm các cặp cung bằng nhau và có số đo nhỏ hơn 180o
d) So sánh hai cung nhỏ \(\overset\frown{AB}\) và \(\overset\frown{CD}\).