Mỗi bánh xe đạp ở Hình 1 gợi nên hình ảnh của một đường tròn.
Hai đường tròn đó có điểm chung hay không?
Mỗi bánh xe đạp ở Hình 1 gợi nên hình ảnh của một đường tròn.

Hai đường tròn đó có điểm chung hay không?
Đồng hồ được mô tả ở Hình 2 có kim phút dài 12 cm. Khi kim phút quay một vòng thì đầu mút của kim phút vạch nên đường gì?

Thảo luận (1)Hướng dẫn giảiKim phút quay một vòng thì đầu mút của kim phút vạch nên đường tròn.
(Trả lời bởi Nguyễn Quốc Đạt)
Hãy chỉ ra một số đồ vật trong thực tiễn gợi nên hình ảnh của đường tròn.
Thảo luận (1)Hướng dẫn giảiMột số đồ vật trong thực tiễn gợi nên hình ảnh của đường tròn là bánh xe, biển báo giao thông, bàn ăn hình tròn, gương trang điểm hình tròn, …
(Trả lời bởi Nguyễn Quốc Đạt)
Quan sát Hình 5.
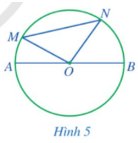
a) So sánh MN và OM + ON.
b) So sánh MN và AB.
Thảo luận (1)Hướng dẫn giảia) Xét tam giác \(OMN\) có \(MN < OM + ON\).
b) Ta có: \(OM = ON = OA = OB = R\).
\( \Rightarrow OM + ON = OA + OB = AB.\)
Mà \(MN < OM + ON\).
\( \Rightarrow MN < AB\).
(Trả lời bởi Nguyễn Quốc Đạt)
Cho tam giác nhọn ABC. Đường tròn tâm O đường kính BC cắt các cạnh AB và AC lần lượt tại M và N. Chứng minh MN < BC.
Thảo luận (1)Hướng dẫn giải
Nối OM, ON.
Xét ∆OMN, ta có: MN < OM + ON (Bất đẳng thức tam giác). (1)
Vì B, M, N, C cùng thuộc đường tròn (O) nên OA = OM = ON = OB.
Ta có: OM + ON = OB + OC.
Lại có BC là đường kính của đường tròn (O) nên BC = OB + OC.
Do đó OM + ON = BC. (2)
Từ (1) và (2) suy ra MN < BC.
(Trả lời bởi Nguyễn Quốc Đạt)
Cho đường tròn (O; R).
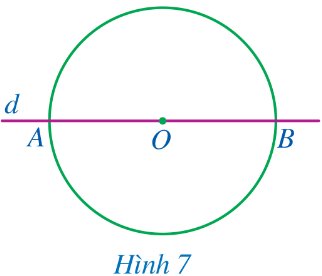
a) Vẽ đường thẳng d đi qua tâm O cắt đường tròn tại A, B. So sánh OA và OB (Hình 7).
b) Giả sử M là một điểm tùy ý trên đường tròn (O; R). Trên tia đối của tia OM, ta lấy điểm N sao cho ON = OM. Điểm N có thuộc đường tròn (O; R) hay không?
Thảo luận (1)Hướng dẫn giảia) \(OA = OB = R\).
b) Do \(OM = R\) lại có \(ON = OM\) nên \(ON = R\). Vậy \(N\) thuộc đường tròn \(\left( {O;R} \right)\).
(Trả lời bởi Nguyễn Quốc Đạt)
Cho đường tròn (O; R). Giả sử d là đường thẳng đi qua tâm O, M là một điểm tùy ý trên đường tròn (O; R). Kẻ MH vuông góc với d tại H. Trên tia MH lấy điểm N sao cho H là trung điểm của MN (ta gọi điểm N là điểm đối xứng với điểm M qua đường thẳng d). Điểm N có thuộc đường tròn (O; R) hay không?
Thảo luận (1)Hướng dẫn giải
Nối OM, ON.
Xét ∆OMH (vuông tại H)và ∆ONH (vuông tại H) ta có:
MH = NH (do H là trung điểm của MN);
OH là cạnh chung.
Do đó ∆OMH = ∆ONH (hai cạnh góc vuông).
Suy ra OM = ON (hai cạnh tương ứng).
Mà M thuộc đường tròn (O; R) nên OM = R nên ON = R, do đó N thuộc đường tròn (O; R).
(Trả lời bởi Nguyễn Quốc Đạt)
Bạn Hoa có một tờ giấy hình tròn. Nêu cách gấp giấy để xác định tâm của hình đó.
Thảo luận (1)Hướng dẫn giảiTa gấp tờ giấy làm đôi sau đó gấp đôi thêm một lần nữa. Giao điểm của hai lần gấp chính là tâm của đường tròn.
(Trả lời bởi Nguyễn Quốc Đạt)
Bạn Đan vẽ năm vòng tròn minh họa cho biểu tượng của Thế vận hội Olympic như ở Hình 10. Hình vẽ đó thể hiện những cặp đường tròn cắt nhau. Theo em, hai đường tròn cắt nhau thì chúng có bao nhiêu điểm chung?

Thảo luận (1)Hướng dẫn giảiHai đường tròn cắt nhau thì chúng có 2 điểm chung.
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hai đường tròn (O; 14 cm), (O’; 5 cm) với OO’ = 8 cm. Hỏi hai đường tròn đó có cắt nhau hay không?
Thảo luận (1)Hướng dẫn giảiTa thấy bán kính của hai đường tròn \(\left( O \right),\left( {O'} \right)\) lần lượt là \(R = 14cm,r = 5cm\).
Do \(R - r = 14 - 5 = 9\left( {cm} \right)\), \(R + r = 14 + 5 = 19\left( {cm} \right)\) và \(9 > 8\) nên \(R - r > OO'\).
Vậy hai đường tròn \(\left( {O;14cm} \right)\) và \(\left( {O'5cm} \right)\) không cắt nhau.
(Trả lời bởi Nguyễn Quốc Đạt)