Question

Trong không gian Oxyz, cho mặt cầu S(I; R) có tâm I(a; b; c) và bán kính R.

Xét một điểm M(x; y; z) thay đổi.

a) Tính khoảng cách IM theo x, y, z và a, b, c.

b) Nêu điều kiện cần và đủ của x, y, z để điểm M(x; y; z) nằm trên mặt cầu S(I; R).

Answer 1

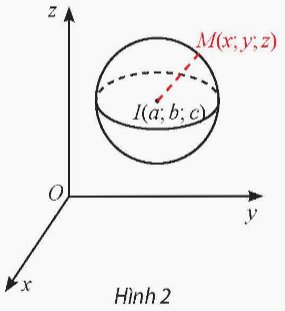
a) Ta có \(I\left( {a;b;c} \right)\) và \(M\left( {x;y;z} \right)\). Suy ra \(IM = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} \).

b) Điều kiện cần và đủ của \(x\), \(y\), \(z\) để điểm \(M\left( {x;y;z} \right)\) nằm trên mặt cầu \(S\left( {I;R} \right)\) là \(IM = R\), điều này tương đương với

\(\sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}}  = R \Leftrightarrow {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).