Question

Tìm cực trị của hàm số \(g\left(x\right)=\dfrac{x^2+x+4}{x+1}\).

Answer 1

Tập xác định: \(D = \mathbb{R}\backslash \{  - 1\} \)

\(g'(x) = \frac{{{x^2} + 2x - 3}}{{{x^2} + 2x + 1}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x =  - 3\end{array} \right.\)

Bảng biến thiên:

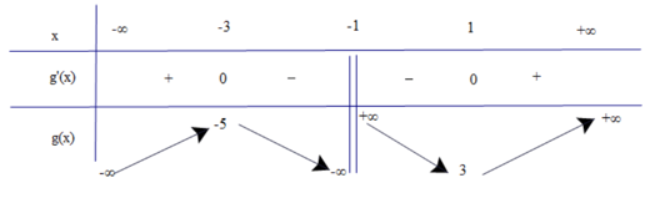
Vậy hàm số đạt cực tiểu tại x = -3, \({y_{ct}} = f( - 3) =  - 5\), đạt cực đại tại x = 1, \({y_{cd}} = f(1) = 3\)