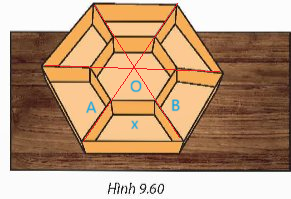
Nối các cặp đỉnh đối diện của lục giác với nhau, ta được điểm O là tâm của hình lục giác lớn và lục giác nhỏ.
Ta chia hình lục giác thành 6 tam giác đều chung đỉnh O, 2 đỉnh còn lại là các đỉnh 2 đỉnh kề nhau của lục giác.
Lấy hai điểm A, B là hai đỉnh kề nhau của lục giác nhỏ như hình vẽ. Đặt AB = x (cm) \(\left( {0 < x < 10} \right)\).
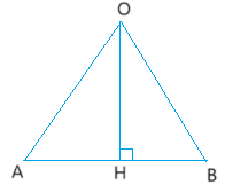
Khi đó \(\Delta AOB\) đều có \(OA = OB = AB = x\) và \(\widehat B = 60^\circ \).
Kẻ \(OH \bot AB\). Dựa vào hệ thức giữa cạnh và góc trong tam giác vuông, ta có:
\(OH = OB.\sin \widehat {OBA} = x.\sin 60^\circ = \frac{{\sqrt 3 }}{2}x\left( {cm} \right)\)
Suy ra \({S_{\Delta AOB}} = \frac{{OH.AB}}{2} = \frac{{\frac{{\sqrt 3 }}{2}x.x}}{2} = \frac{{{x^2}\sqrt 3 }}{4}\left( {c{m^2}} \right)\)
Ta có diện tích hình lục giác đều nhỏ là:
Slục giác đều nhỏ \( = 6.{S_{\Delta AOB}} = 6.\frac{{{x^2}\sqrt 3 }}{4} = \frac{{3\sqrt 3 {x^2}}}{2}\left( {c{m^2}} \right)\).
Theo đề bài, diện tích lục giác đều nhỏ bằng hai lần diện tích mỗi hình thang nên diện tích mỗi hình thang là:
Shình thang = Slục giác đều nhỏ : 2 = \(\frac{{3\sqrt 3 {x^2}}}{2}:2 = \frac{{3\sqrt 3 {x^2}}}{4}\left( {c{m^2}} \right)\),
suy ra tổng diện tích 6 hình thang là: \(6.\frac{{3\sqrt 3 {x^2}}}{4} = \frac{{9\sqrt 3 {x^2}}}{2}\left( {c{m^2}} \right)\)
Do đó, diện tích lục giác đều lớn là:
Slục giác đều lớn = Slục giác đều nhỏ + S6 hình thang \( = \frac{{3\sqrt 3 {x^2}}}{2} + \frac{{9\sqrt 3 {x^2}}}{2} = \frac{{12\sqrt 3 {x^2}}}{2} = 6\sqrt 3 {x^2}\left( {c{m^2}} \right)\) (1)
Mà tương tự như Slục giác đều nhỏ, ta cũng có thể tính được diện tích lục giác đều theo độ dài cạnh của nó theo công thức \(S = \frac{{3\sqrt 3 {x^2}}}{2}\left( {c{m^2}} \right)\) với x là độ dài cạnh.
Suy ra Slục giác đều lớn \( = \frac{{3\sqrt 3 {{.10}^2}}}{2} = 150\sqrt 3 \left( {c{m^2}} \right)\) (2)
Từ (1) và (2), ta có phương trình: \(6\sqrt 3 {x^2} = 150\sqrt 3 \)
suy ra \({x^2} = 25\), do đó \(x = 5\)(thỏa mãn vi \(0 < x < 10\)).
Vậy cạnh của lục giác đều nhỏ là 5cm.