Question

Gọi I là giao điểm ba đường phân giác của tam giác ABC. Vẽ ID, IE, IF lần lượt vuông góc với các cạnh BC, AC và AB (Hình 7).

a) Chứng minh rằng IE = IF = ID.

b) Vẽ đường tròn tâm I bán kính IE. Có nhận xét gì về vị trí của đường tròn này với ba cạnh của tam giác ABC?

Answer 1

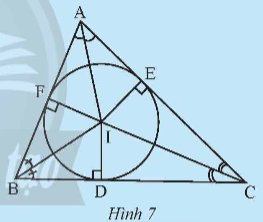
a) Xét tam giác FBI vuông tại F và tam giác DBI vuông tại D có:

\(\widehat {FBI} = \widehat {IBD}\) (do BI là phân giác góc \(\widehat {FBD}\));

IB chung.

Suy ra \(\Delta \) FBI = \(\Delta \) DBI (cạnh huyền – góc nhọn).

Nên IF = ID (hai cạnh tương ứng) (1).

Xét \(\Delta \) IDC vuông tại D và \(\Delta \) IEC vuông tại E có:

\(\widehat {DCI} = \widehat {IEC}\) (do IC là phân giác góc \(\widehat {DEC}\));

IC chung.

Suy ra \(\Delta \) IDC = \(\Delta \) IEC (cạnh huyền – góc nhọn).

Nên ID = IE (hai cạnh tương ứng) (2).

Từ (1) và (2) suy ra  IE = IF = ID.

b) Đường tròn này tiếp xúc với ba cạnh của tam giác tại các điểm F, D, E.