Bài 8. Giao thoa sóng

GIAO THOA SÓNG

1. Giao thoa sóng 

a. Hiện tượng

Hiện tượng giao thoa sóng cơ được mô tả như hình

Ta quan sát thấy trong vùng gặp nhau (vùng giao thoa) của hai sóng xuất hiện những điểm mà tại đó mặt nước dao động mạnh và những điểm mà tại đó mặt nước tĩnh lặng (đứng yên không dao động).

Hiện tượng trên được gọi là hiện tượng giao thoa sóng.

b. Điều kiện để có giao thoa sóng

• Hai nguồn phát sóng phải là hai nguồn kết hợp.
• Hai nguồn kết hợp là hai nguồn dao động cùng phương, cùng tần số, cùng pha hoặc có độ lệch pha không đổi theo thời gian.

2. Khảo sát sự giao thoa của hai nguồn cùng pha

Xét hai nguồn sóng \(S_1\) và \(S_2\) có phương trình dao động là: \(u_1=u_2=A\cos(\omega t)\). Sóng do hai nguồn tạo ra lan truyền trên mặt phẳng như hình vẽ dưới.

   

Điểm M cách \(S_1\), \(S_2\) lần lượt là \(d_1\), \(d_2\)

• Phương trình truyền sóng do \(S_1\rightarrow M\): \(u_{1M}=A\cos(\omega t-\dfrac{2\pi d_1}{\lambda})\)
• Phương trình sóng do \(S_2\rightarrow M\): \(u_{2M}=A\cos(\omega t-\dfrac{2\pi d_2}{\lambda})\)

Như vậy, điểm M nhận 2 dao động do \(S_1\) và \(S_2\) truyền đến, phương trình dao động của M là tổng hợp của 2 dao động này:

 \(u_M=u_{1M}+u_{2M}\)\(=A\cos(\omega t-\dfrac{2\pi d_1}{\lambda})+ A\cos(\omega t-\dfrac{2\pi d_2}{\lambda})\)

 \(\Rightarrow u_M=2A\cos[\dfrac{\pi(d_2-d_1)}{\lambda}]\cos[\omega t-\dfrac{\pi (d_2+d_1)}{\lambda}]\\ \qquad\qquad \color{red}{\vdash\qquad \ \ A_M \qquad\dashv} \)

Nhận xét:

•  Biên độ dao động của \(M\) là \(A_M=2A\cos[\dfrac{\pi(d_2-d_1)}{\lambda}]\)
• Điểm M dao động với biên độ cực đại là \(2A\) khi \(|\cos[\dfrac{\pi(d_2-d_1)}{\lambda}]|=1\) \(\Leftrightarrow \boxed{ d_2-d_1=k\lambda}\)(1) (sóng do 2 nguồn truyền đến cùng pha nhau)
• Điểm M dao động với biên độ cực tiểu là \(0\) khi \(\cos[\dfrac{\pi(d_2-d_1)}{\lambda}]=1\) \(\Leftrightarrow \boxed{ d_2-d_1=(k+0,5)\lambda}\)(2) (sóng do 2 nguồn truyền đến ngược pha)

3. Hình ảnh giao thoa

Trước hết, ta biết rằng tập hợp các điểm cách 2 điểm cho trước \(S_1, S_2\) một khoảng \(d_1,d_2\) và thoả mãn \(d_2-d_1=2a=const\) (3) là đường Hypebol nhận \(S_1,S_2\) là tiêu điểm.

Từ phương trình (1) và (2) ở trên, nếu ta cho \(k\) những giá trị xác định thì được dạng như phương trình (3). Do vậy, tập hợp những điểm M có biên độ cực đại (cực tiểu) là những Hypebol nhận \(S_1, S_2\) làm tiêu điểm.

Tập hợp các đường Hypebol được biểu diễn trên hình vẽ sau: 

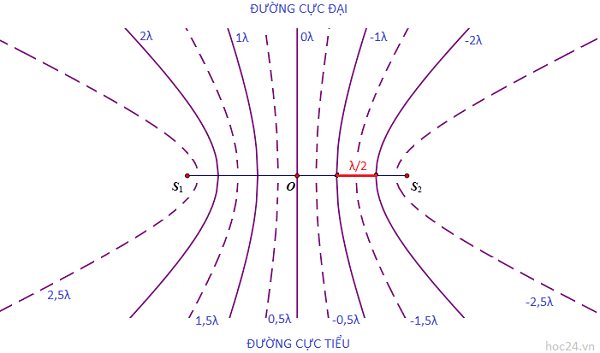
Lưu ý:

• Ta gọi các đường cực đại (cực tiểu) là các vân cực đại (cực tiểu).
• Trung trực của \(S_1S_2\) là vân cực đại, trung điểm \(O\) dao động với biên cực đại.
• Giao của các vân cực đại với đoạn \(S_1S_2\)là những điểm dao động với biên độ cực đại. Giao của vân cực tiểu với \(S_1S_2\) là những điểm cực tiểu (không dao động).
• Tại vị trí 2 nguồn \(S_1\), \(S_2\) nhận dao động cưỡng bức từ bên ngoài (kích thích để tạo sóng) nên 2 điểm này không có cực đại, cực tiểu.
• Ta dễ dàng chứng minh được khoảng cách giữa hai cực đại (hoặc cực tiểu) liên tiếp trên đoạn \(S_1S_2\) là \(\dfrac{\lambda}{2}\)

4. Bài tập ví dụ

Câu 1: Hai điểm \(S_1\), \(S_2\) trên mặt một chất lỏng dao động cùng pha với pha ban đầu bằng 0, biên độ 1,5 cm và tần số \(f\) = 20 Hz. Vận tốc truyền sóng trên mặt chất lỏng là 1,2 m/s. Điểm \(M\) cách \(S_1\), \(S_2\)  các khoảng lần lượt bằng 30cm và 36cm. Viết phương trình dao động của \(M\).

Giải:

Bước sóng: \(\lambda=\dfrac{v}{f}=\dfrac{120}{20}=6\,\)(cm/s)

Phương trình dao động của nguồn: \(u_1=u_2=1,5.\cos(40\pi t)\)(cm)

Áp dụng phương trình dao động tổng hợp: \(u=2Acos[\dfrac{\pi(d_2 - d_1)}{\lambda}].cos[\omega t-\dfrac{\pi(d_1 + d_2)}{\lambda}]\)

Ta được: \(u=2.1,5.\cos(\dfrac{\pi(30 - 36)}{6}).\cos(40\pi t-\dfrac{\pi(30+36)}{6})\)(cm)

\(\Rightarrow u=3.cos(\pi).cos(40\pi t-11\pi)=-3cos(40\pi t-11\pi)=3cos(40\pi t-10\pi)\)(cm)

Vậy \(u=-3cos(40\pi t)\,\)(cm). 

Câu 2: Trong giao thoa sóng trên mặt nước, hai nguồn kết hợp \(A,B\) dao động cùng pha, cùng tần số \(f\)= 16 Hz. Tại một điểm \(M\) trên mặt nước cách các nguồn \(A,B\) những khoảng \(d_1\) = 30 cm, \(d_2\) = 25,5 cm, sóng có biên độ cực đại. Giữa \(M\) và đường trung trực \(AB\) có hai dãy cực đại khác. Tính vận tốc truyền sóng trên mặt nước.

Giải:

\(M\) nằm trên đường cực đại và giữa \(M\) và đường trung trực \(AB\) có hai dãy cực đại khác nên ta suy ra M nằm trên đường cực đại số 3.

⇒ \(d_2 – d_1 = –3\lambda\) hay \(30 – 25,5 = 3\lambda\) \(\Rightarrow λ = 1,5\) (cm)

Từ đó suy ra \(v = λ.f = 1,5.16 = 24\) (cm/s).