Bài 8. Lặp với số lần chưa biết trước
Nội dung lý thuyết
BÀI 8: LẶP VỚI SỐ LẦN CHƯA BIẾT TRƯỚC
1. Các hoạt động lặp với số lần chưa biết trước
a. Ví dụ 1:
- Một ngày, Long quyết định cứ 10 phút gọi điện một lần cho Trang cho đến khi nào có người nhấc máy.
=> Chưa thể biết trước được số lần lặp tối đa. Điều kiện để kết thúc hoạt động lặp đó là có người nhấc máy.
b. Ví dụ 2:
- Nếu cộng lần lượt n số tự nhiên đầu tiên (n = 1, 2, 3,...), ta sẽ được các kết quả:
- T1 = 1
- T2 = 1 + 2
- T3 = 1 + 2 + 3
=> Cần cộng bao nhiêu số tự nhiên đầu tiên để ta nhận được tổng Tn nhỏ nhất lớn hơn 1000?
- Phân tích bài toán:
|
n |
Tổng Tn |
Điều kiện Tn ≤ 1000 |
|
1 |
Tn = 1 |
Đúng |
|
2 |
Tn = 1 + 2 |
Đúng |
|
3 |
Tn = 1 + 2 + 3 |
Đúng |
|
... |
... |
Đúng |
|
? |
Tn = 1 + 2 + 3 + ... + ? Sao cho Tn nhỏ nhất >1000 |
Sai, Kết thúc việc tính tổng. |
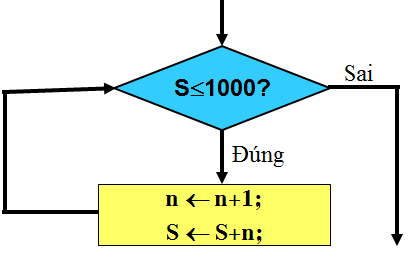
- Mô tả thuật toán: Kí hiệu S là tổng cần tìm và ta có thuật toán như sau:
- Bước 1. S \(\leftarrow\) 0, n \(\leftarrow\) 0.
- Bước 2. Nếu S ≤ 1000, n \(\leftarrow\) n + 1; ngược lại chuyển tới bước 4.
- Bước 3. S \(\leftarrow\) S + n và quay lại bước 2.
- Bước 4. In kết quả: S và n là số tự nhiên nhỏ nhất sao cho S > 1000. Kết thúc thuật toán.
- Nhận xét: Để viết chương trình chỉ dẫn máy tính thực hiện các hoạt động lặp như trong các ví dụ trên, ta có thể sử dụng câu lệnh có dạng lặp với số lần chưa biết trước.
2. Ví dụ về lệnh lặp với số lần chưa biết trước
- Trong Pascal câu lệnh lặp với số lần chưa biết trước có dạng:
while <điều kiện> do <câu lệnh>
- Trong đó:
- Điều kiện thường là một phép so sánh;
- Câu lệnh có thể là câu lệnh đơn giản hay câu lệnh ghép.
- Câu lệnh lặp này được thực hiện như sau:
- Bước 1: Kiểm tra điều kiện.
- Bước 2: Nếu điều kiện SAI, câu lệnh sẽ bị bỏ qua và việc thực hiện lệnh lặp kết thúc. Nếu điều kiện đúng, thực hiện câu lệnh và quay lại bước 1.
Ví dụ 3:
While a<=b do a:=a+1;
- Trong đó:
- While, do là các từ khóa.
- Điều kiện là a<=b (chứa phép so sánh).
- Câu lệnh là a:=a+1 (câu lệnh đơn).
Ví dụ 4:
While a>b do
Begin
write(‘a>b’);
a:=a-1;
End;
- Trong đó:
- while, do là các từ khóa.
- Điều kiện lặp là a > b (chứa phép so sánh).
- Câu lệnh là Write(‘a>b’) và a:=a-1 (câu lệnh ghép).
Ví dụ 5:
- Yêu cầu: Dùng câu lệnh lặp While … Do để viết chương trình thể hiện thuật toán trong Ví dụ 2
var S,n: integer;
Begin
S:=0;
n:=0;
while S<=1000 do begin
n:=n+1;
S:=S+n;
end;
write(‘Tong S= ’,S,‘ va ’,n,’ la so tu nhien nho nhat sao cho S>1000’);
Readln;
End.
Ví dụ 6:
- Yêu cầu: Với giá trị nào của n (n>0) thì \(\frac{1}{n}\) nhỏ hơn 1 sai số cho trước ví dụ: \(\frac{1}{n}< 0,005\) hoặc \(\frac{1}{n}< 0,003\)?
uses crt;
var x: real; n: integer;
const sai_so=0.003;
begin
clrscr;
x:=1; n:=1;
while x>=sai_so do
begin
n:=n+1;
x:=1/n;
end;
writeln('So n nho nhat de 1/n < ',sai_so:5:4, 'la ',n);
readln;
end.
3. Lặp vô hạn lần – Lỗi lập trình cần tránh
- Khi viết chương trình sử dụng cấu trúc lặp cần chú ý tránh tạo nên vòng lặp không bao giờ kết thúc.
- Ví dụ 1 chương trình lặp vô hạn như sau:
var a:integer;
begin
a:=5;
while a<6 do writeln('A');
end.