Bài 5: Diện tích xung quanh của hình lăng trụ đứng

1. Công thức tính diện tích xung quanh

Diện tích xung quanh của một hình lăng trụ đứng là tổng diện tích của các mặt bên.

Ví dụ 1: Xét hình lăng trụ đứng tứ giác \(ABCD.A'B'C'D'\): 

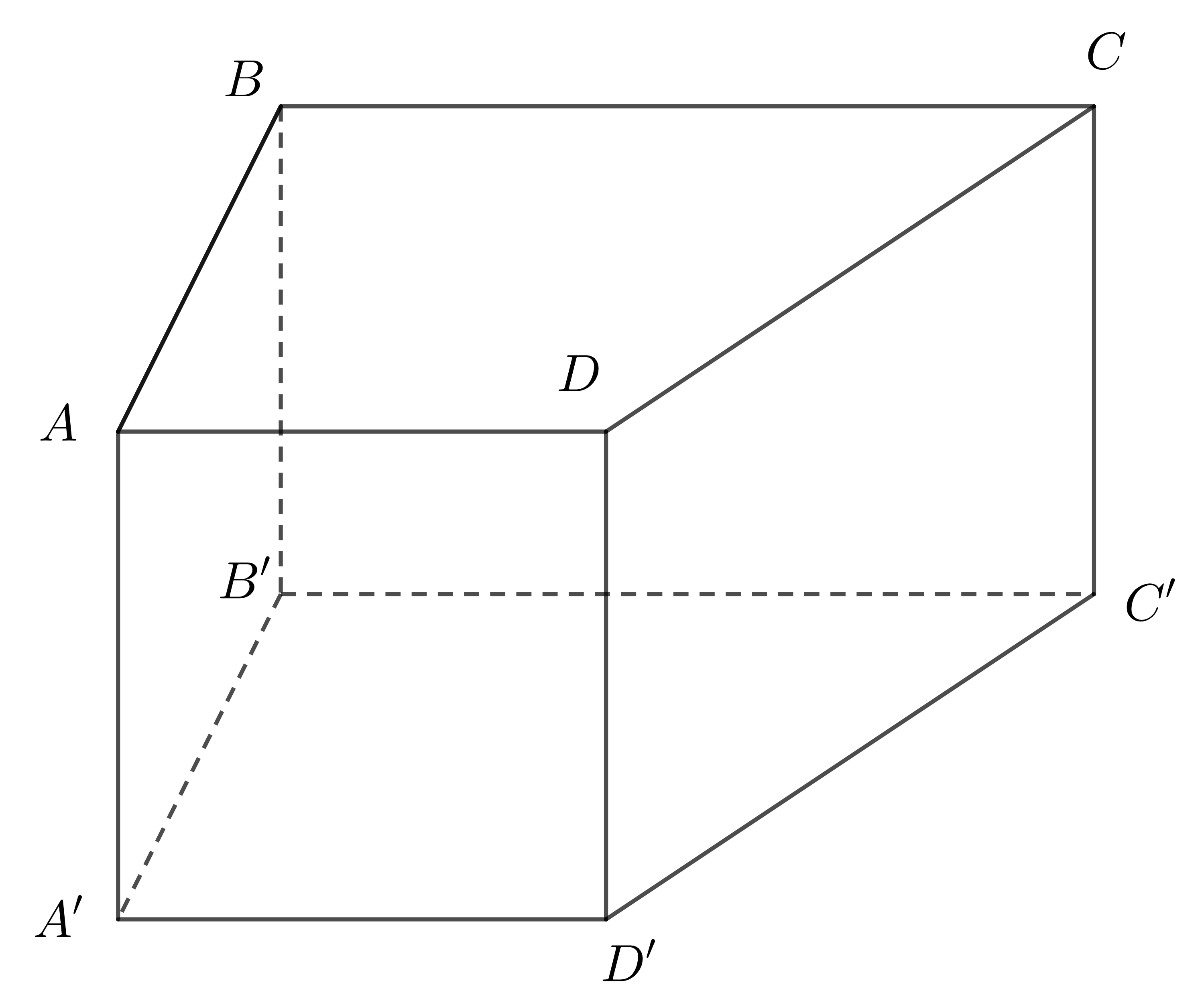
Diện tích xung quanh của lăng trụ đứng trên được tính bằng: \(S_{ABB'A'}+S_{BCC'B'}+S_{CDD'C'}+S_{DAA'D'}\)

Do \(ABB'A'\) là hình chữ nhật nên \(S_{ABB'A'}=AA'.AB\)

Tương tự: \(S_{BCC'B'}=BB'.BC\) ; \(S_{CDD'C'}=CC'.CD\) ; \(S_{DAA'D'}=DD'.AD\)

Mặt khác \(AA'=BB'=CC'=DD'=h\) chính là chiều cao của hình lăng trụ đứng

Suy ra \(S_{ABB'A'}+S_{BCC'B'}+S_{CDD'C'}+S_{DAA'D'}=h\left(AB+BC+CD+DA\right)\)

Lại có: \(AB+BC+CD+DA\) chính là chu vi đáy \(ABCD\)

Như vậy: Diện tích xung quanh của lăng trụ đứng trên bằng chu vi đáy nhân với chiều cao.

Ví dụ 2: Xét hình lăng trụ đứng tam giác \(ABC.A'B'C'\):

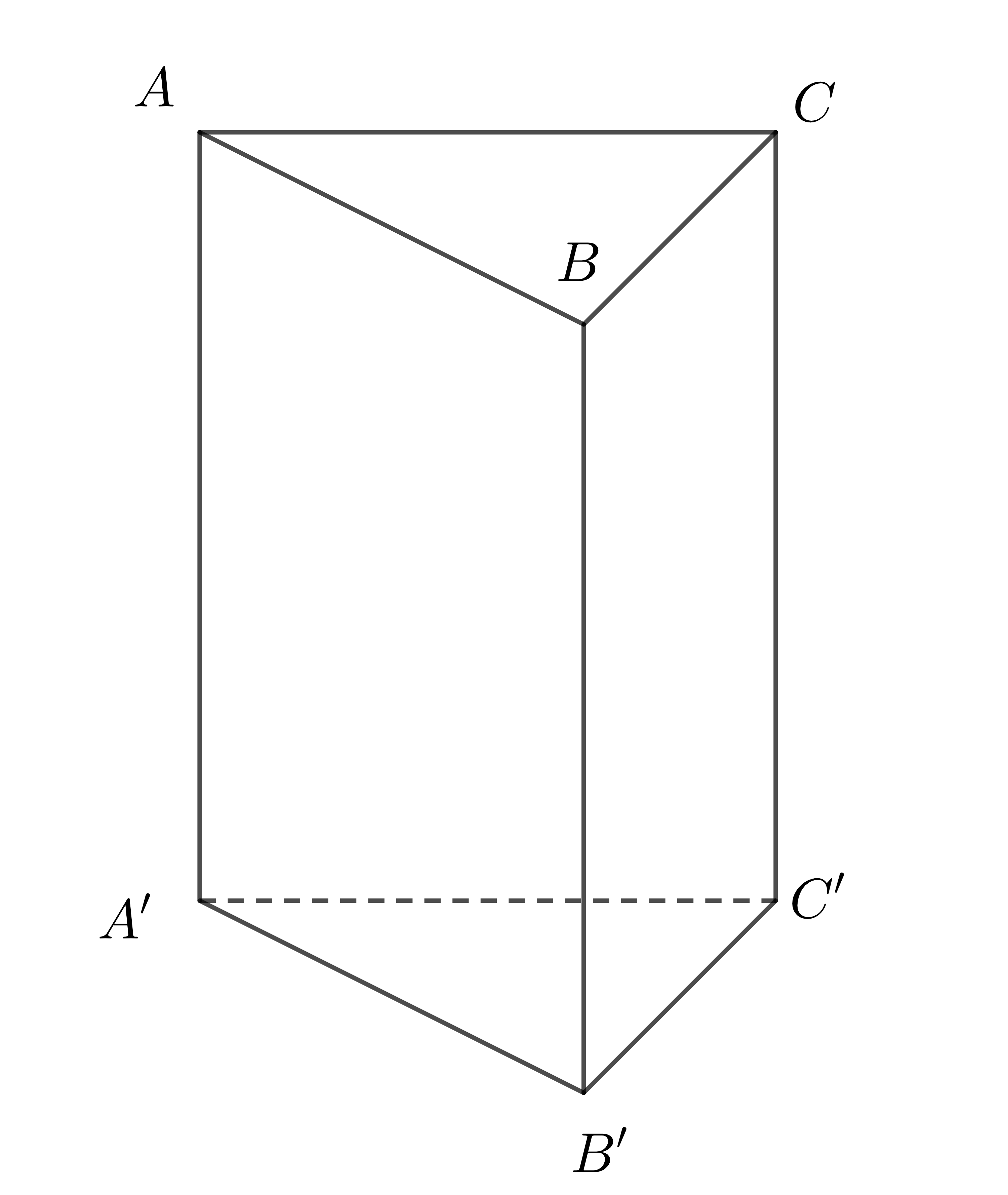
Gọi chiều cao hình lăng trụ trên là \(h'\) thì \(AA'=BB'=CC'=h'\)

Diện tích xung quanh hình lăng trụ trên được tính bằng:

     \(S_{ABB'A'}+S_{BCC'B'}+S_{CAA'C'}\)

     \(=AA'.AB+BB'.BC+CC'.AC\)

     \(=h'.AB+h'.BC+h'.AC\)

     = \(=h'.\left(AB+BC+AC\right)\)

Lại có: \(AB+BC+CA\) chính là chu vi đáy \(ABC\)

Như vậy: Diện tích xung quanh hình lăng trụ đứng trên cũng được tính bằng chu vi đáy nhân với chiều cao.

Từ đó ta rút ra công thức:

- Diện tích xung quanh của hình lăng trụ đứng bằng chu vi đáy nhân với chiều cao.

         \(S_{xq}=2p.h\)

   (\(p\) là nửa chu vi đáy, \(h\) là chiều cao)

- Diện tích toàn phần của hình lăng trụ đứng bằng diện tích xung quanh cộng với diện tích hai đáy.

       \(S_{tp}=S_{xq}+2.S_đ\)

2. Các ví dụ

Ví dụ 1: Cho hình lăng trụ đứng có các kích thước như hình vẽ. Tính diện tích xung quanh của hình đó.

Giải:

Chu vi đáy của hình lăng trụ trên là: \(2+3+5+6=16\left(cm\right)\)

Diện tích xung quanh của hình lăng trụ trên là: \(16.4,5=72\left(cm^2\right)\)

Ví dụ 2: Một hình lăng trụ đứng tam giác \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(A\) và \(AB=4cm,AC=3cm\). Biết rằng chiều cao lăng trụ đứng trên là \(9cm\).

    a) Tính diện tích xung quanh của lăng trụ đứng trên?

    b) Tính diện tích toàn phần của lăng trụ đứng trên?

Giải:

a) Áp dụng định lí Py-ta-go trong tam giác vuông \(ABC\) ta có: \(AB^2=AC^2=BC^2\)

    \(\Rightarrow BC^2=AB^2+AC^2=3^2+4^2=25\)

    \(\Rightarrow BC=5\left(cm\right)\)

  Chu vi đáy \(ABC\) là: \(P_{ABC}=3+4+5=12\left(cm\right)\)

  Diện tích xung quanh hình lăng trụ là: \(S_{xq}=12.9=108\left(cm^2\right)\)

b) Diện tích mỗi đáy của hình lăng trụ là: \(\dfrac{1}{2}.3.4=6\left(cm^2\right)\)

   Diện tích toàn phần của hình lăng trụ là: \(S_{tp}=108+2.6=120\left(cm^2\right)\)

Ví dụ 3: Một lăng trụ tam giác đều có cạnh đáy dài \(3,5cm\) và diện tích xung quanh là \(115,5cm^2\). Tính chiều cao lăng trụ trên?

Giải:

Do đáy của hình lăng trụ là tam giác đều nên chu vi đáy là: \(3,5+3,5+3,5=10,5\left(cm\right)\)

Gọi chiều cao lăng trụ là \(h\) (cm)

Diện tích xung quanh lăng trụ là \(115,5cm^2\)

Suy ra \(10,5.h=115,5\) \(\Rightarrow h=\dfrac{115,5}{10,5}=11\left(cm\right)\)

Vậy chiều cao lăng trụ đó là 11 cm.

Ví dụ 4: Một hình hộp chữ nhật có kích thước đáy chữ nhật là \(15cm\times10cm\). Biết rằng diện tích xung quanh bằng tổng diện tích hai đáy. Tính chiều cao hình hộp chữ nhật đó?

Giải:

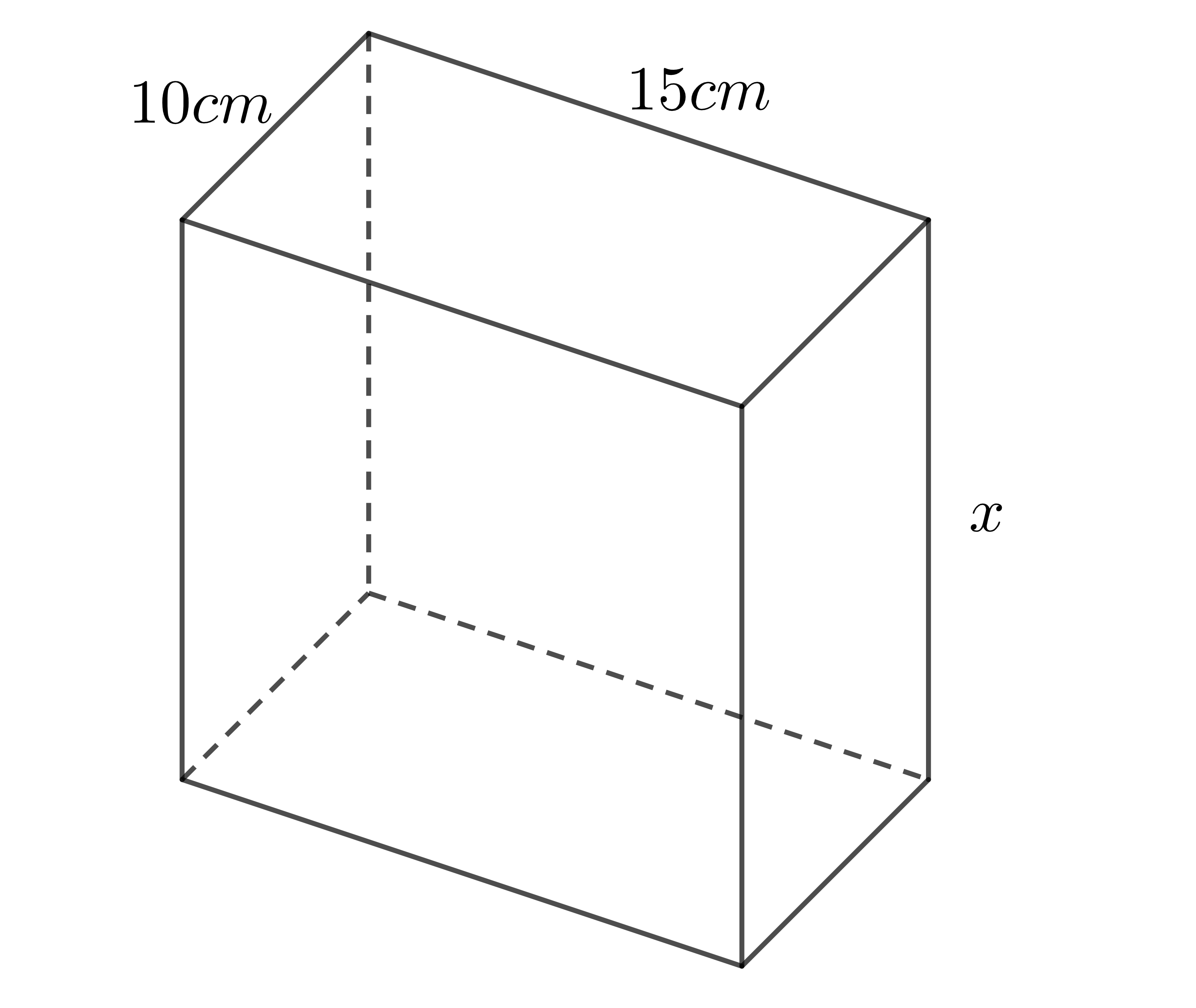
Gọi chiều cao hình hộp là \(x\left(cm\right)\)

Diện tích 2 đáy là: \(2.10.15=300\left(cm^2\right)\)

Chu vi đáy là: \(2.\left(10+15\right)=50\left(cm\right)\)

Nên diện tích xung quanh là: \(50x\left(cm^2\right)\)

Theo đề bài ta có: \(50x=300\)

\(\Rightarrow x=6\left(cm\right)\)

Vậy chiều cao hình hộp chữ nhật là \(6cm\).

Ví dụ 5: Một phòng học hình hộp chữ nhật có chiều dài \(5,5m\), chiều rộng \(4,5m\), chiều cao \(3,2m\). Phòng có hai cửa ra vào hình chữ nhật kích thước \(1,2m\times2m\) và bốn cửa sổ hình vuông cạnh \(1,5m\). Người ta dự định sơn toàn bộ trần nhà và xung quanh tường. Tính diện tích cần sơn?

Giải:

Diện tích trần nhà là: \(5,5.4,5=24,75\left(m^2\right)\)

Chu vi nền nhà là: \(2.\left(5,5+4,5\right)=20\left(m\right)\)

Diện tích xung quanh phòng là: \(20.3,2=64\left(m^2\right)\)

Diện tích hai cửa ra vào là: \(2.1,2.2=4,8\left(m^2\right)\)

Diện tích bốn cửa sổ là: \(4.1,5.1,5=9\left(m^2\right)\)

Diện tích cần sơn là: \(64+24,75-4,8-9=74,95\left(m^2\right)\)