Bài 3. Giá trị tuyệt đối của một số thực

I. Khái niệm

Khoảng cách từ điểm x đến điểm gốc 0 trên trục số được gọi là giá trị tuyệt đối của số x, kí hiệu là \(|x|\).

Chú ý:

+ Giá trị tuyệt đối của một số luôn là một số không âm: \(|x| \geq0\) với mọi số thực x.

+ Hai số thực đối nhau có giá trị tuyệt đối bằng nhau.

Ví dụ 1: Tìm giá trị tuyệt đối của mỗi số thực sau: \(-1;\dfrac{1}{5};0.\)

Hướng dẫn giải

Ta biểu diễn trên trục số:

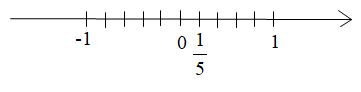
Căn cứ vào khoảng cách từ mỗi điểm \(-1;\dfrac{1}{5};0\) đến điểm gốc 0 trên trục số, ta có

\(|-1|=1\\ \Big|\dfrac{1}{5}\Big|=\dfrac{1}{5}\\ |0|=0 \)

II. Tính chất

+ Nếu x là số dương thì giá trị tuyệt đối của x là chính nó:\(|x|=x(x>0).\)

+ Nếu x là số âm thì giá trị tuyệt đối của x là số đối của nó:

\(|x|=-x(x<0).\)

+ Giá trị tuyệt đối của 0 là 0: \(|0|=0.\)

Nhận xét: Với mỗi số thực x ta có

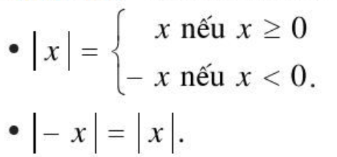
Ví dụ 2: Tìm

a) \(|\sqrt{11}|\);                  b) \(\Big|\dfrac{-3}{4}\Big|\).

Hướng dẫn giải

a) \(|\sqrt{11}|=\sqrt{11}.\)

b) \(\Big|\dfrac{-3}{4}\Big|=\dfrac{3}{4}.\)

Ví dụ 3: Tìm số thực x biết

a) \(|x|=15\);

b) \(|x-12|=0.\)

c) \(|x+1|=-1\).

Hướng dẫn giải

a) \(|x|=15\) nên x = 15 hoặc x = -15.

b) \(|x-12|=0\) nên x - 12 = 0 hay x = 12.

c) Do \(|x+1|\geq0\) với mọi số thực x nên không có số thực nào thỏa mãn \(|x+1|=-1\).

Ví dụ 4: Trên trục số, hãy tính độ dài của đoạn thẳng AB trong mỗi trường hợp sau:

a)

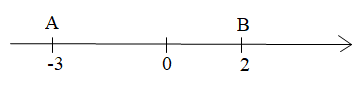
b)

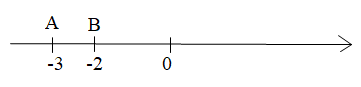
Hướng dẫn giải

Ta có

a) AB = OA + OB = |-3| + |2| = 3 + 2 = 5.

b) AB = OA - OB = |-3| - |-2| = 3 - 2 = 1.

Chú ý: Giả sử hai điểm A và B lần lượt biểu diễn hai số thực a và b khác nhau trên trục số. Khi đó, độ dài của đoạn thẳng AB là |a - b| tức là AB = |a - b|.