§2. Phương trình đường tròn

1. Phương trình đường tròn có tâm và bán kính cho trước

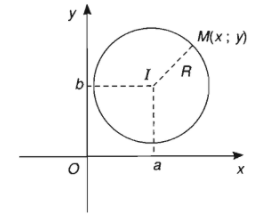
Trong mặt phẳng \(Oxy\) cho đường thẳng \(\left(C\right)\) tâm \(I\left(a;b\right)\), bán kính \(R\).

Ta có \(M\left(x;y\right)\in\left(C\right)\Leftrightarrow IM=R\)

                                  \(\Leftrightarrow\sqrt{\left(x-a\right)^2+\left(y-b\right)^2}=R\)

                                  \(\Leftrightarrow\left(x-a\right)^2+\left(y-b\right)^2=R^2\)

Phương trình \(\left(x-a\right)^2+\left(y-b\right)^2=R^2\) được gọi là phương trình đường tròn tâm \(I\left(a;b\right)\) bán kính \(R\).

Chẳng hạn, phương trình đường tròn tâm \(I\left(2;-3\right)\) bán kính \(R=5\) là: \(\left(x-2\right)^2+\left(y+3\right)^2=25\)

Ví dụ 1: Cho hai điểm \(A\left(1;2\right)\) và \(B\left(-3;4\right)\). Viết phương trình đường tròn \(\left(C\right)\) đường kính \(AB\).

Giải:

Gọi \(I\) là trung điểm của đoạn thẳng \(AB\). Ta có \(I\left(-1;3\right)\)

Bán kính của đường tròn \(\left(C\right)\) là \(IA=\sqrt{\left(-1-1\right)^2+\left(3-2\right)^2}=\sqrt{5}\)

Như vậy ta được đường tròn \(\left(C\right)\) tâm \(I\left(-1;3\right)\) bán kính \(R=\sqrt{5}\)

Suy ra phương trình đường tròn \(\left(C\right)\) là: \(\left(x+1\right)^2+\left(y-3\right)^2=5\).

Ví dụ 2: Viết phương trình đường tròn tâm \(I\left(2;-3\right)\) và đi qua điểm \(M\left(-2;3\right)\).

Giải:

Với \(I\left(2;-3\right)\), \(M\left(-2;3\right)\) ta có \(IM=\sqrt{\left(2+2\right)^2+\left(-3-3\right)^2}=\sqrt{52}\)

Đường tròn tâm \(I\) và đi qua điểm \(M\) có bán kính \(R=IM=\sqrt{52}\)

Do đó ta có phương trình đường tròn là: \(\left(x-2\right)^2+\left(y+3\right)^2=52\).

Ví dụ 3: Tìm tâm và bán kính của các đường tròn sau:

    a) \(x^2+y^2-2x-2y-2=0\)  ;

    b) \(16x^2+16y^2+16x-8y-11=0\)

Giải:

a) Ta có: \(x^2+y^2-2x-2y-2=0\) \(\Leftrightarrow\left(x-1\right)^2+\left(y-1\right)^2=4\)

Vậy đường tròn này có tâm \(I\left(1;1\right)\) và bán kính \(R=2\).

b) Ta có: \(16x^2+16y^2+16x-8y-11=0\) 

          \(\Leftrightarrow x^2+y^2+x-\dfrac{1}{2}y-\dfrac{11}{16}=0\)

         \(\Leftrightarrow\left(x+\dfrac{1}{2}\right)^2+\left(y-\dfrac{1}{4}\right)^2=1\)

Vậy đường tròn này có tâm \(I\left(-\dfrac{1}{2};\dfrac{1}{4}\right)\) bán kính \(R=1\).

Chú ý: Phương trình đường tròn có tâm là gốc toạ độ \(O\) và có bán kính \(R\) là: 

                   \(x^2+y^2=R^2\)

2. Nhận xét

Phương trình đường tròn \(\left(x-a\right)^2+\left(y-b\right)^2=R^2\) có thể được viết dưới dạng \(x^2+y^2-2ax-2by+c=0\) , trong đó \(c=a^2+b^2-R^2\).

Ngược lại, phương trình \(x^2+y^2-2ax-2by+c=0\) là phương trình của đường tròn \(\left(C\right)\) khi và chỉ khi \(a^2+b^2-c>0\). Khi đó đường tròn \(\left(C\right)\) có tâm \(I\left(a;b\right)\) và bán kính \(R=\sqrt{a^2+b^2-c}\).

Ta xét lại ví dụ 3 trên nhưng với cách làm khác.

Ví dụ 3: Tìm tâm và bán kính của các đường tròn sau:

    a) \(x^2+y^2-2x-2y-2=0\)  ;

    b) \(16x^2+16y^2+16x-8y-11=0\)

Giải:

a) Ta có \(x^2+y^2-2x-2y-2=0\) \(\Leftrightarrow\) \(x^2+y^2-2.1.x-2.1y-2=0\)

Suy ra phương trình trên có các hệ số \(a=1,b=1,c=-2\)

Nên đường tròn có tâm \(I\left(1;1\right)\) và bán kính \(R=\sqrt{1^2+1^2-\left(-2\right)}=\sqrt{4}=2\)

b) Ta có \(16x^2+16y^2+16x-8y-11=0\) \(\Leftrightarrow x^2+y^2+x-\dfrac{1}{2}y-\dfrac{11}{16}=0\)

             \(\Leftrightarrow x^2+y^2-2.\dfrac{-1}{2}.x-2.\dfrac{1}{4}.y-\dfrac{11}{16}=0\)

Suy ra phương trình trên có các hệ số \(a=-\dfrac{1}{2},b=\dfrac{1}{4},c=-\dfrac{11}{16}\)

Nên đường tròn có tâm \(I\left(-\dfrac{1}{2};\dfrac{1}{4}\right)\), bán kính \(R=\sqrt{\left(-\dfrac{1}{2}\right)^2+\left(\dfrac{1}{4}\right)^2-\left(-\dfrac{11}{16}\right)}=1\)

Ví dụ 4: Viết phương trình đường tròn \(\left(C\right)\) đi qua 3 điểm \(A\left(1;2\right)\), \(B\left(5;2\right)\) và \(C\left(1;-3\right)\).

Giải:

Gọi phương trình đường tròn \(\left(C\right)\) là \(x^2+y^2-2ax-2by+c=0\)

Do \(A\left(1;2\right)\in\left(C\right)\) nên ta có \(1^2+2^2-2.a.1-2.b.2+c=0\) \(\Rightarrow2a+4b-c=5\)  (1)

Do \(B\left(5;2\right)\in\left(C\right)\) nên ta có \(5^2+2^2-2.a.5-2.b.2+c=0\) \(\Rightarrow10a+4b-c=29\)  (2)

Do \(C\left(1;-3\right)\in\left(C\right)\) nên ta có \(1^2+\left(-3\right)^2-2.a.1-2.b.\left(-3\right)+c=0\) \(\Rightarrow2a-6b-c=10\) (3)

Từ (1), (2) và (3) ta có hệ phương trình \(\left\{{}\begin{matrix}2a+4b-c=5\\10a+4b-c=29\\2a-6b-c=10\end{matrix}\right.\)

Giải hệ phương trình trên ta được nghiệm \(a=3,b=-\dfrac{1}{2},c=-1\)

Thay vào ta được phương trình đường tròn \(\left(C\right)\) là \(x^2+y^2-6x+y-1=0\).

3. Phương trình tiếp tuyến của đường tròn

Cho điểm \(M_0\left(x_0;y_0\right)\) nằm trên đường tròn \(\left(C\right)\) tâm \(I\left(a;b\right)\).

Gọi \(\Delta\) là tiếp tuyến với \(\left(C\right)\) tại \(M_0\).

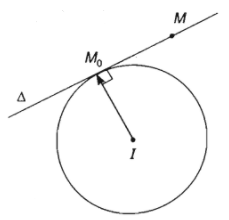
Ta có \(M_0\) thuộc \(\Delta\) và vectơ \(\overrightarrow{IM_0}=\left(x_0-a;y_0-b\right)\) là vectơ pháp tuyến của \(\Delta\).

Do đó \(\Delta\) có phương trình là:

            \(\left(x_0-a\right)\left(x-x_0\right)+\left(y_0-b\right)\left(y-y_0\right)=0\)        (2)

Phương trình (2) là phương trình tiếp tuyến của đường tròn \(\left(x-a\right)^2+\left(y-b\right)^2=R^2\) tại điểm \(M_0\) nằm trên đường tròn.

Ví dụ 5: Viết phương trình tiếp tuyến tại điểm \(M\left(3;4\right)\) thuộc đường tròn \(\left(C\right):\left(x-1\right)^2+\left(y-2\right)^2=8\).

Giải:

Từ phương trình \(\left(x-1\right)^2+\left(y-2\right)^2=8\) ta suy ra \(\left(C\right)\) có tâm \(I\left(1;2\right)\) 

Suy ra phương trình tiếp tuyến với \(\left(C\right)\) tại \(M\left(3;4\right)\) là

         \(\left(3-1\right)\left(x-3\right)+\left(4-2\right)\left(y-4\right)=0\)

     \(\Leftrightarrow2x+2y-14=0\)

     \(\Leftrightarrow x+y-7=0\)

Vậy phương trình tiếp tuyến với \(\left(C\right)\) tại \(M\left(3;4\right)\) là \(x+y-7=0\).