có thể có phân số a/b (a,b thuộc \(ℤ\), b \(\ne\)0 ) sao cho :
a/b =a.m/b.n (m ,n thuộc\(ℤ\); m ,n khác 0 và m không bằng n) hay không ?
Những câu hỏi liên quan
có thể có phân số \(\frac{a}{b}\)(a,b thuộc \(ℤ\), b \(\ne\)0 ) sao cho :
\(\frac{a}{b}=\frac{a.m}{b.n}\)(m ,n thuộc\(ℤ\); m ,n khác 0 và m không bằng n) hay không ?
không thể, vì để có phân số mới bằng phân số a/b thì m=n và n khác 0
Đúng 0
Bình luận (0)
có nhưng chỉ với a=0
còn a khác thì ko đc!
Đúng 0
Bình luận (0)
Có thể có phân số a/b(a,b thuộc z,b khác 0 )
a/b=a.m/b.n(m,n thuộc z;m,n khác0 và m khác n) hay ko
có thể có phân số a/b (a, b thuộc Z, b khác 0) sao cho
a/b=a.m/b.n (m,n thuộc Z; m,n khác 0 và m khác n) hay không?
không có vì nếu a/b=a.m/b.n thì chia 2 vế cho a/b ta được 1=m/n hay m=n (trái giả thiết)
Đúng 0
Bình luận (0)
Có thể có phân số a/b vs a,b thuộc Z, b khác 0 sao cho:
a/b=a.m/b.m
Vs m,n thuộc Z, m,n khác 0 & m khác n
Giúp mk đi
Nhanh lên nha, mk cần cấp tốc
Ai giúp sẽ là bạn của mk , còn được mk k cho & cuối cùng là tôn làm thầy dạy của mk
Đúng 0
Bình luận (0)
có thể có phân số a phần b (a, b thuộc z, b khác 0) sao cho
a phần b= a.m phần b.m (m,n thuộc z;m,n khác 0 và m khác n) hay ko
\(\frac{a}{b}\)= \(\frac{a.m}{b.n}\)(m, n \(\in\)Z ; m, n \(\ne\)0; m \(\ne\)n) xảy ra khi a = 0.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
có thể có phân số a/b(a,b thuộc Z,b khác 0) sao cho
a/b=a.m/b.m(m,n thuộc Z;m,n khác 0 và m khác n)
Giải cụ thể nha bạn.
bấm vào đúng 0 sẽ ra kết quả, mình làm bài này rồi dễ lắm bạn ạ
Đúng 0
Bình luận (0)
Có thể có phân số \(\dfrac{a}{b},\left(a,b\in\mathbb{Z},b\ne0\right)\) sao cho :
\(\dfrac{a}{b}=\dfrac{a.m}{b.n},\left(m,n\in\mathbb{Z};m,n\ne0,m\ne n\right)\) hay không ?
Có thể có phân số a/b (a, b ∈ Z, b ≠ 0) sao cho:
(m, n ∈ Z, m , n ≠ 0 , m ≠ n) khi và chỉ khi a = 0
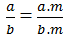
Vì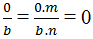 
(m, n ∈ Z, m , n ≠ 0 , m ≠ n)
Đúng 0
Bình luận (0)
Tìm a/b biết a/b=a.m/b.n (m,n thuộc Z)và (n không bằng 0: m không bằng n)
theo đề bài
=> a/b = an/bn = am/bn
<=> an/bn - am/bn = 0
<=> a.( n - m) / bn = 0
<=> a (n-m) = 0
Do n khác m -> n - m khác 0
=> a = 0
=> a/b = 0
Đúng 0
Bình luận (0)
Giải:
Theo đề bài, ta có: a/b = a . m/b . n (m, n thuộc Z) và (n không bằng 0; m không bằng n)
Ta được quyền suy ra: a/b = a . n/b . = a . m/ b . m
=> a . n/ a . m/b . m = 0
=> a.(n - m) / b . n = 0
=> a.(n - m) = 0
Do n không bằng (hoặc khác) m => n - m sẽ khác 0
=> a = 0
=> a/b cũng = 0
Đúng 0
Bình luận (0)
Giả sử
m
-
a
b
,
a
,
b
∈
ℤ
*
,
(
a
,
b
)
1
là giá trị thực của tham số m để đường thẳng
d
:
y
-
3
x
+
m
cắt đồ thị hàm số
y
2
x
+...
Đọc tiếp
Giả sử m = - a b , a , b ∈ ℤ * , ( a , b ) = 1 là giá trị thực của tham số m để đường thẳng d : y = - 3 x + m cắt đồ thị hàm số y = 2 x + 1 x - 1 (C) tại hai điểm phân biệt A,B sao cho trọng tâm tam giác OAB thuộc đường thẳng ∆ : x - 2 y - 2 = 0 với O là gốc tọa độ. Tính a+2b.
A. 2
B. 5
C. 11
D. 21
