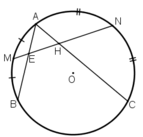
Cho (O) và hai dây AB,AC. Gọi M,N lần lượt là điểm chính giữa của \(\widebat{AB}\);\(\widebat{AC}\). đường thẳng MN cắt dây AB tại D, cắt dây AC tại E. Chứng minh tam giác ADE cân

Những câu hỏi liên quan
Cho đường tròn (O) và 2 dây AB,AC sao cho AB<AC và O nằm trong góc BAC. Gọi M, N lần lượt là điểm chính giữa \(\widebat{AB}\)và \(\widebat{AC}\).
MN cắt dây AB ở H, BN cắt CM tại K
a) C/m : tam giác NCK cân và Tam giác AMK cân
b) C/m : tứ giác BMHK nội tiếp
c) C/m : HK // AC và so sánh góc BAK và góc CAK
Cho đường tròn (O) lấy 3 điểm A, B, C. Gọi M, N, P lần lượt là các điểm chính giữa của các cung \(\widebat{AB},\widebat{BC},\widebat{AC}\). Gọi I, K, J lần lượt là giao điểm của AB và MN, AN và BP, AC và NP. Cmr:
a) \(\Delta CNJ\) là tam giác cân
b) \(IK//BC\)
c) I, K, J thẳng hàng
Cho đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của cung AB và cung AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh tam giác AEH là tam giác cân.
+ Do góc  là góc có đỉnh bên trong đường tròn chắn hai cung
là góc có đỉnh bên trong đường tròn chắn hai cung 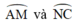
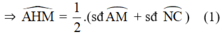
+ Do góc  là góc có đỉnh bên trong đường tròn chắn hai cung
là góc có đỉnh bên trong đường tròn chắn hai cung 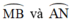
+ Do M và N là điểm chính giữa của cung A B ⏜ v à A C ⏜
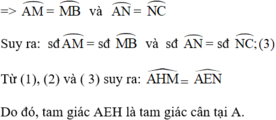
Đúng 1
Bình luận (0)
Cho đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của cung AB và cung AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh tam giác AEH là tam giác cân.
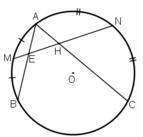
+ Do góc  là góc có đỉnh bên trong đường tròn chắn hai cung
là góc có đỉnh bên trong đường tròn chắn hai cung ![]()
![]()
+ Do góc  là góc có đỉnh bên trong đường tròn chắn hai cung
là góc có đỉnh bên trong đường tròn chắn hai cung 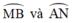

Kiến thức áp dụng
+ Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
Đúng 0
Bình luận (0)
Cho đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của cung AB và AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh tam giác AEH là tam giác cân.
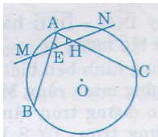
Ta có: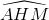 =
=  (1)
(1)
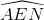 =
= ![]() (2)
(2)
(Vì 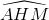 và
và 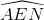 là các góc có đỉnh cố định ở bên trong đường tròn).
là các góc có đỉnh cố định ở bên trong đường tròn).
Theo gỉả thiết thì:

Từ (1),(2), (3), (4), suy ra 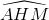 =
= 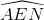 do đó ∆AEH là tam giác cân.
do đó ∆AEH là tam giác cân.
Đúng 0
Bình luận (0)
Cho đường tròn (O), dây AB cố định, điểm C thay đổi trên cung lớn AB sao cho tam giác ABC nhọn. Gọi M, N lần lượt là điểm chính giữa các cung AC và AB. Gọi I là giao điểm của BM và CN. Gọi H, K lần lượt là giao điểm của MN với AC và AB. 1) Chứng minh: tam giác NIB là tam giác cân 2)Gọi D là giao điểm của CN với AB. Chứng minh: HI//AB và CH/CACA/AD. 3)...
Đọc tiếp
Cho đường tròn (O), dây AB cố định, điểm C thay đổi trên cung lớn AB sao cho tam giác ABC nhọn. Gọi M, N lần lượt là điểm chính giữa các cung AC và AB. Gọi I là giao điểm của BM và CN. Gọi H, K lần lượt là giao điểm của MN với AC và AB. 1) Chứng minh: tam giác NIB là tam giác cân 2)Gọi D là giao điểm của CN với AB. Chứng minh: HI//AB và CH/CA=CA/AD. 3)Xác định vị trí điểm C trên cung lớn AB để diện tích tứ giác AIBN lớn nhất
Cho nửa đường tròn $(O)$ đường kính $AB$ và dây cung AC. Gọi $M$, $N$ lần lượt là các điểm chính giữa của các cung $AC$ và $BC$. Hai dây $AN$ và $BM$ cắt nhau tại $I$. Chứng minh $CI$ là tia phân giác của góc $ACB$.
BHA=90 BHB=90
ta có góc CBM là góc nội tiếp chắn cung CM
góc MBA là góc nội tiếp chắn cung MA
mà cung CM= cung MA( vì M là điểm chính giữa của cung CA)
=> góc CBM= góc MBA
hay BM là tia phân giác của góc CBA
CM tương tự ta có: AN là tia phân giác của góc CAB
xét tam giác CAB có
2 tia phân giác BM và AN cắt nhau tại I
=> I là tâm đường tròn nội tiếp tam giác CAB
=> CI là tia phân giác của góc ACB(đpcm)
ta có góc CBM là góc nội tiếp chắn cung CM
góc MBA là góc nội tiếp chắn cung MA
mà cung CM= cung MA( vì M là điểm chính giữa của cung CA)
=> góc CBM= góc MBA
hay BM là tia phân giác của góc CBA
CM tương tự ta có: AN là tia phân giác của góc CAB
xét tam giác CAB có
2 tia phân giác BM và AN cắt nhau tại I
=> I là tâm đường tròn nội tiếp tam giác CAB
=> CI là tia phân giác của góc ACB(đpcm)
Xem thêm câu trả lời
Cho đường tròn (O) ngoại tiếp tam giác nhọn ABC. Gọi M và N lần lượt là điểm chính giữa của cung nhỏ AB và cung nhỏ BC. Hai dây AN và CM cắt nhau tại điểm I. Dây MN cắt các cạnh AB và BC lần lượt tại các điểm H và K.2) Chứng minh
N
B
2
N
K
.
N
M
.
Đọc tiếp
Cho đường tròn (O) ngoại tiếp tam giác nhọn ABC. Gọi M và N lần lượt là điểm chính giữa của cung nhỏ AB và cung nhỏ BC. Hai dây AN và CM cắt nhau tại điểm I. Dây MN cắt các cạnh AB và BC lần lượt tại các điểm H và K.
2) Chứng minh N B 2 = N K . N M .
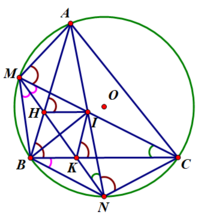
2) Chứng minh N B 2 = N K . N M .
Ta có N là điểm chính giữa cung B C ⏜ ⇒ B N ⏜ = C N ⏜ ⇒ B M N ^ = C M N ^ (góc nội tiếp chắn 2 cung bằng nhau)
Mà C B N ^ = C M N ^ (góc nội tiếp chắn cùng chắn cung C N ⏜ )
C B N ^ = B M N ^ (cùng bằng góc C M N ^ ) ⇒ K B N ^ = B M N ^
Xét Δ K B N v à Δ B M N có:
N ^ chung
K B N ^ = B M N ^
⇒ Δ K B N ∽ Δ B M N ⇒ K N B N = B N M N ⇒ N B 2 = N K . N M
(điều phải chứng minh).
Đúng 0
Bình luận (0)
Cho đường tròn (O) ngoại tiếp tam giác nhọn ABC . Gọi M và N lần lượt là điểm chính giữa của cung nhỏ AB và cung nhỏ BC . Hai dây AN và CM cắt nhau tại điểm I . Dây MN cắt cạnh AB và BC lần lượt tại các điểm H và K
1. Chứng minh 4 điểm C , N , K . I cùng thuộc 1 đường tròn
2. Chứng minh NB^2 = NK.NM













