cho x=2017 tính
y=f(x)=x5-2018*x4+2018*x3-2018*x2+2018*x-1
Những câu hỏi liên quan
Cho biểu thức
f
(
x
)
1
2018
x
+
2018
. Tính tổng
S
2018
[
f
(
-
2017
)
+
f
(
-
2016
)
+
.
.
.
...
Đọc tiếp
Cho biểu thức f ( x ) = 1 2018 x + 2018 . Tính tổng
S = 2018 [ f ( - 2017 ) + f ( - 2016 ) + . . . + f ( 0 ) + f ( 1 ) + . . . + f ( 2018 ) ]
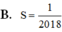
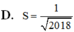
Một bạn nhờ mình đăng hộ ( phan thuy anh )
Tìm N(2017) biết đa thức N(x)=x2017−2018.x2016+2018.x2015−2018.x2014+........−2018.x2+2018.x−1
Tinh nhanh:
2017 2017 2017 x 2018 2018 2018 2018 /2018 2018 2018 x 2017 2017 2017 2017
1. Cho biểu thức B :
\(B=x^{2017}-2018.x^{2016}+2018.x^{2015}-2018.x^{2014}+...-2018.x^2+2018.x-1\)
TÍNH GIÁ TRỊ BIỂU THỨC VỚI x=2017
Tinh nhanh:
2017 2017 2017 x 2018 2018 2018 2018 /2018 2018 2018 x 2017 2017 2017 2017
Giúp mình nha!!!!!!!!!!!
\(=\frac{2018}{2017}\)
~~~~~~~~~~~ai đi ngang qua nhớ để lại k ~~~~~~~~~~~~~
~~~~~~~~~~~~ Chúc bạn sớm kiếm được nhiều điểm hỏi đáp ~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~ Và chúc các bạn trả lời câu hỏi này kiếm được nhiều k hơn ~~~~~~~~~~~~
Đúng 0
Bình luận (0)
giải ra hộ mình nha các bạn ra kết quả như thế là sai rùi thử tính máy tính đi
Đúng 0
Bình luận (0)
Tìm N(2017) biết đa thức N(x)=\(x^{2017}-2018.x^{2016}+2018.x^{2015}-2018.x^{2014}+........-2018.x^2+2018.x-1\)
Ta có: \(N\left(x\right)=x^{2017}-2018x^{2016}+2018x^{2015}-...-2018x^2+2018x-1\)
\(=x^{2017}-2018\left(x^{2016}-x^{2015}+...+x^2-x\right)-1\)
\(\Rightarrow N\left(2017\right)=2017^{2017}-2018\left(2017^{2016}-2017^{2015}+...+2017^2-2017\right)-1\)
Đặt \(A=2017^{2016}-2017^{2015}+...+2017^2-2017\)
\(\Rightarrow2017A=2017^{2017}-2017^{2016}+...+2017^3-2017^2\)
\(\Rightarrow2018A=2017^{2017}-2017\)
\(\Rightarrow A=\dfrac{2017^{2017}-2017}{2018}\)
\(\Rightarrow N\left(2017\right)=2017^{2017}-2018.\dfrac{2017^{2017}-2017}{2018}-1\)
\(=2017^{2017}-\left(2017^{2017}-2017\right)-1\)
\(=2017^{2017}-2017^{2017}+2017-1\)
\(=2016\)
Vậy N(2017) = 2016
Đúng 0
Bình luận (1)
A = 2017/2018 x 7/8 + 2017/2018 x 3/8 - 2017/2018 x 1/4
Ta có : A =\(\frac{2017}{2018}\)x \(\frac{7}{8}\)+ \(\frac{2017}{2018}\)x \(\frac{3}{8}\)- \(\frac{2017}{2018}\)x \(\frac{1}{4}\)
= \(\frac{2017}{2018}\) x ( \(\frac{7}{8}+\frac{3}{8}-\frac{1}{4}\))
= \(\frac{2017}{2018}\)x 1
=\(\frac{2017}{2018}\)
Vậy A= : \(\frac{2017}{2018}\)
Bài giải
\(A=\frac{2017}{2018}\text{ x }\frac{7}{8}+\frac{2017}{2018}\text{ x }\frac{3}{8}-\frac{2017}{2018}\text{ x }\frac{1}{4}\)
\(A=\frac{2017}{2018}\text{ x }\frac{1}{4}\left(\frac{7}{2}+\frac{3}{2}-1\right)=\frac{2017}{2018}\text{ x }\frac{1}{4}\text{ x }4==\frac{2017}{2018}\text{ x }1=\frac{2017}{2018}\)
Tính bằng cách thuận tiện:
A = 2017/2018 x 7/8 + 2017/2018 x 3/8 - 2017/2018 x 1/4
Cho hàm số f(x)=x-
1
x
Với x khác 0. Chứng tỏ rằng [f(2018)]2017+[f(1
2018)]2017 =0