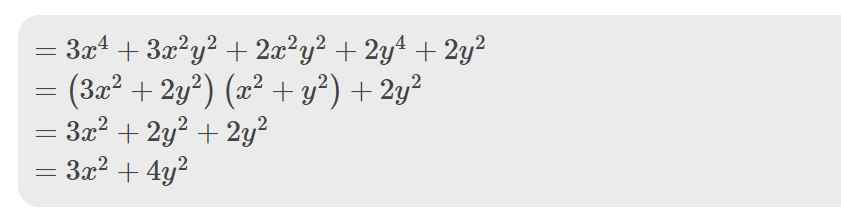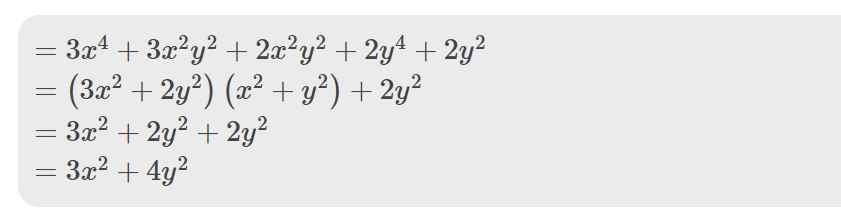<=> m = (2x-1).(2y-1)

<=> m = 2x.2y + 2x.(-1) + (-1).2y +(-1).(-1)

<=> m = 4xy - 2x - 2y +1

<=> m = 4xy - 2.(x-y) +1

thế x + y = 10 và xy bằng 16 vào biểu thức ta dc

 m = 4.16 - 2.10 +1

=> m = 45

vậy giá trị của biểu thức là m = 45

x^2=a;y^2=b(Đk:a,b không âm)
Từ giả thiết suy ra a+b=2
=>3x^4+5x^2y^2+2y^4+2y^2
=3a^2+5ab+2b^2+2b
=(3a^2+3ab)+(2ab+2b^2)+2b
=3a(a+b)+2b(a+b)+2b
=(a+b)(3a+2b)+2b
=2(3a+2b)+2b
=2(2a+2b)+2a+2b
=4.2+2*\.2=12

Đặt x^2=a;y^2=b(với Đk:a,b không âm) 
Từ giả thiết suy ra a+b=2 
=>3x^4+5x^2y^2+2y^4+2y^2 
=3a^2+5ab+2b^2+2b 
=(3a^2+3ab)+(2ab+2b^2)+2b 
=3a(a+b)+2b(a+b)+2b 
=(a+b)(3a+2b)+2b 
=2(3a+2b)+2b 
=2(2a+2b)+2a+2b 
=4.2+2.2=12

x^2+y^2=1 ma ban

43 nhé bạn

cach lm dau

ta có M=2xy-2x-2y-1=2x16-(2x+2y)-1=32-2(x+y)-1=32-20-1=11( sr nhé)

a) 

\(\hept{\begin{cases}\left(x^2-9x\right)^2\ge0\\!y-2!\ge0\end{cases}\Rightarrow GTNN=10}\) đẳng thức đạt được khi y=2 và \(\orbr{\begin{cases}x=0\\x=9\end{cases}}\)

b) 

cách 1: ghép tạo số hạng (x-2015)

E=x^9(x-2015)+x^8(x-2015)+....+x(x-2015)+x-1=2014 tại x=2015

hoặc

x^10-1=(x-1)(x^9+x^8+..+1) cái này cơ bản

-2014x^9-2014x-2014+2014 thêm 2014 bớt 2014

(x^9+x^8+..+1)(x-1-2014)+2014=(x-2015)(x^9+..+1)+2014=2014

\(A=\frac{1}{2}x^4+x^2y^2+\frac{1}{2}y^4-2x^2y^2\)

\(=\frac{1}{2}\left(x^4-2x^2y^2+y^4\right)=\frac{1}{2}\left(x^2-y^2\right)^2=\frac{1}{2}.4^2=8\)